第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2024 安徽黄山校级质检,中]如图,在四边形 ABCD 中,AB = CD,BA 和 CD 的延长线交于点 E,若点 P 使得$ S_{△PAB} = S_{△PCD},$则满足此条件的点 P(
A.有且只有 1 个
B.有且只有 2 个
C.组成∠E 的平分线
D.组成∠E 的平分线所在的直线和∠E 的外角平分线所在的直线(点 E 除外)
D
)A.有且只有 1 个
B.有且只有 2 个
C.组成∠E 的平分线
D.组成∠E 的平分线所在的直线和∠E 的外角平分线所在的直线(点 E 除外)
答案:
D [解析]作∠E及∠E的外角的平分线所在直线,当点P在任意一条角平分线所在直线上时,可得点P到直线AB和CD的距离相等.因为AB=CD,所以此时点P满足S△PAB=S△PCD,故满足条件的点P组成∠E的平分线所在的直线和∠E的外角平分线所在的直线(E点除外).故选D.
如图,P 是△ABC 的三条角平分线的交点,连接 PA,PB,PC,若△PAB,△PBC,△PAC 的面积分别为$ S_1,S_2,S_3,$则(
$A. S_1 < S_2 + S_3$
$B. S_1 = S_2 + S_3$
$C. S_1 > S_2 + S_3$
D. 无法确定$ S_1 $与$ S_2 + S_3 $的大小
A
)$A. S_1 < S_2 + S_3$
$B. S_1 = S_2 + S_3$
$C. S_1 > S_2 + S_3$
D. 无法确定$ S_1 $与$ S_2 + S_3 $的大小
答案:
A 添加辅助线已知三角形三条角平分线的交点,通常过这个交点作三边的垂线段,根据角平分线的性质得到线段相等.易错警示:本题易受“三角形三条角平分线的交点到三角形三边的距离相等”的影响,认为满足条件的货物中转站只有1处,其实三角形两条外角平分线的交点到其三边的距离也相等,这样可供选择的地址有4处。[解析]过点P作PD⊥AB于D,PE⊥AC于E,PF⊥BC于F,如图
∵P是△ABC的三条角平分线的交点,PD⊥AB,PE⊥AC,PF⊥BC,
∴PD=PE=PF.
∵S₁=$\frac{1}{2}$·AB·PD,S₂=$\frac{1}{2}$·BC·PF,S₃=$\frac{1}{2}$·AC·PE,
∴S₂+S₃=$\frac{1}{2}$·(AC+BC)·PD.
∵AB<AC+BC,
∴$\frac{1}{2}$·AB·PD<$\frac{1}{2}$(AC+BC)·PD,
∴S₁<S₂+S₃.故选A.
∵P是△ABC的三条角平分线的交点,PD⊥AB,PE⊥AC,PF⊥BC,
∴PD=PE=PF.
∵S₁=$\frac{1}{2}$·AB·PD,S₂=$\frac{1}{2}$·BC·PF,S₃=$\frac{1}{2}$·AC·PE,
∴S₂+S₃=$\frac{1}{2}$·(AC+BC)·PD.
∵AB<AC+BC,
∴$\frac{1}{2}$·AB·PD<$\frac{1}{2}$(AC+BC)·PD,
∴S₁<S₂+S₃.故选A.
3 [中]如图,直线 a,b,c 表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
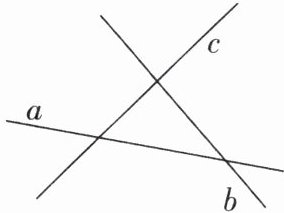
A.1 处
B.2 处
C.3 处
D.4 处
D
)
A.1 处
B.2 处
C.3 处
D.4 处
答案:
D [解析]如图,
∵△ABC三条内角平分线的交点到三角形三边的距离相等,
∴△ABC三条内角平分线的交点O满足条件. 点P是△ABC两条外角平分线的交点,过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边所在直线的距离相等,
∴△ABC两条外角平分线的交点到其三边所在直线的距离相等,满足这种条件的点有3个(P,M,N). 综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4处,故选D.
∵△ABC三条内角平分线的交点到三角形三边的距离相等,
∴△ABC三条内角平分线的交点O满足条件. 点P是△ABC两条外角平分线的交点,过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边所在直线的距离相等,
∴△ABC两条外角平分线的交点到其三边所在直线的距离相等,满足这种条件的点有3个(P,M,N). 综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4处,故选D.
4 [2025 安徽芜湖校级期中,较难]如图,直线 MN⊥PQ,垂足为 O,点 A 是射线 OP 上一点,以 OA 为边在 OP 右侧作∠AOF = 24°,若点 B 是射线 ON 上的一个动点(不与点 O 重合),连接 AB,作△AOB 的两个外角平分线交于点 C,在点 B 的运动过程中,当 CF 取最小值时,∠OFC 的度数为______。
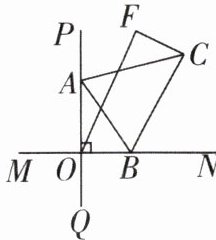

69°
答案:
69° [解析]如图,作CE⊥PQ于E,CG⊥MN于G,CH⊥AB于H,连接OC.
∵AC平分∠PAB,CE⊥PQ,CH⊥AB,
∴CE=CH.同理可得CG=CH,
∴CE=CG,
∴OC平分∠AOB,即点C在∠AOB的平分线上.
∵MN⊥PQ,
∴∠AOB=90°,
∴∠AOC=45°,
∵∠AOF=24°,
∴∠FOC=45°−24°=21°.作FC'⊥OC于C',则C'F≤CF,即当CF取最小值时,点C与C'重合.
∵∠FC'O=90°,
∴∠OFC'=90°−21°=69°,
∴当CF取最小值时,∠OFC的度数为69°.故答案为69°.
∵AC平分∠PAB,CE⊥PQ,CH⊥AB,
∴CE=CH.同理可得CG=CH,
∴CE=CG,
∴OC平分∠AOB,即点C在∠AOB的平分线上.
∵MN⊥PQ,
∴∠AOB=90°,
∴∠AOC=45°,
∵∠AOF=24°,
∴∠FOC=45°−24°=21°.作FC'⊥OC于C',则C'F≤CF,即当CF取最小值时,点C与C'重合.
∵∠FC'O=90°,
∴∠OFC'=90°−21°=69°,
∴当CF取最小值时,∠OFC的度数为69°.故答案为69°.
5 [较难]如图,四边形 ABDC 中,∠D = ∠ABD = 90°,点 O 为 BD 的中点,且 AO 平分∠BAC。
(1)求证:CO 平分∠ACD;
(2)求证:OA⊥OC;
(3)判断 AB,CD,AC 之间的数量关系,并说明理由。
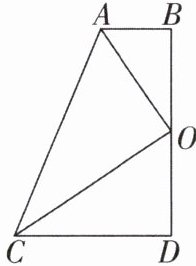
(1)求证:CO 平分∠ACD;
(2)求证:OA⊥OC;
(3)判断 AB,CD,AC 之间的数量关系,并说明理由。

答案:
(1)[证明]如图,过点O作OE⊥AC于E,
∵∠ABD=90°,OE⊥AC,AO平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD.
∵∠D=90°,OE⊥AC,
∴CO平分∠ACD.
(2)[证明]在Rt△ABO和Rt△AEO中,{OA=OA,OB=OE},
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE.同理可得∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=$\frac{1}{2}$×180°=90°,
∴OA⊥OC.
(3)[解]AB+CD=AC.理由:
∵Rt△ABO≌Rt△AEO,
∴AB=AE.同理可得CD=CE.
∵AC=AE+CE,
∴AB+CD=AC.
(1)[证明]如图,过点O作OE⊥AC于E,
∵∠ABD=90°,OE⊥AC,AO平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD.
∵∠D=90°,OE⊥AC,
∴CO平分∠ACD.
(2)[证明]在Rt△ABO和Rt△AEO中,{OA=OA,OB=OE},
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE.同理可得∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=$\frac{1}{2}$×180°=90°,
∴OA⊥OC.
(3)[解]AB+CD=AC.理由:
∵Rt△ABO≌Rt△AEO,
∴AB=AE.同理可得CD=CE.
∵AC=AE+CE,
∴AB+CD=AC.
(1)如图(1),当点 D 是 BC 边上的中点时,$S_{△ABD} : S_{△ACD} = $
(2)如图(2),当 AD 是∠BAC 的平分线时,若 AB = m,AC = n,求$ S_{△ABD} : S_{△ACD} $的值(用含 m,n 的代数式表示);
[解]如图(2),过D作DE⊥AB于E,DF⊥AC于F.
∵AD为∠BAC的平分线,
∴DE=DF.
∵AB=m,AC=n,
∴S△ABD:S△ACD=($\frac{1}{2}$×AB×DE):($\frac{1}{2}$×AC×DF)=$\frac{m}{n}$.
(3)如图(3),AD 平分∠BAC,延长 AD 到 E,使得 AD = DE,连接 BE,如果 AC = 2,AB = 4,$S_{△BDE} = 6,试求 S_{△ABC} $的值。
[解]
∵AD=DE,
∴由(1)知S△ABD:S△EBD=1:1.
∵S△BDE=6,
∴S△ABD=6.
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=S△ACD+S△ABD=3+6=9.
1:1
;(2)如图(2),当 AD 是∠BAC 的平分线时,若 AB = m,AC = n,求$ S_{△ABD} : S_{△ACD} $的值(用含 m,n 的代数式表示);
[解]如图(2),过D作DE⊥AB于E,DF⊥AC于F.
∵AD为∠BAC的平分线,
∴DE=DF.
∵AB=m,AC=n,
∴S△ABD:S△ACD=($\frac{1}{2}$×AB×DE):($\frac{1}{2}$×AC×DF)=$\frac{m}{n}$.
(3)如图(3),AD 平分∠BAC,延长 AD 到 E,使得 AD = DE,连接 BE,如果 AC = 2,AB = 4,$S_{△BDE} = 6,试求 S_{△ABC} $的值。
[解]
∵AD=DE,
∴由(1)知S△ABD:S△EBD=1:1.
∵S△BDE=6,
∴S△ABD=6.
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=S△ACD+S△ABD=3+6=9.
答案:
(1)1:1;
(2)[解]如图
(2),过D作DE⊥AB于E,DF⊥AC于F.
∵AD为∠BAC的平分线,
∴DE=DF.
∵AB=m,AC=n,
∴S△ABD:S△ACD=($\frac{1}{2}$×AB×DE):($\frac{1}{2}$×AC×DF)=$\frac{m}{n}$.
(3)[解]
∵AD=DE,
∴由
(1)知S△ABD:S△EBD=1:1.
∵S△BDE=6,
∴S△ABD=6.
∵AC=2,AB=4,AD平分∠CAB,
∴由
(2)知S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=S△ACD+S△ABD=3+6=9.
(1)1:1;
(2)[解]如图
(2),过D作DE⊥AB于E,DF⊥AC于F.
∵AD为∠BAC的平分线,
∴DE=DF.
∵AB=m,AC=n,
∴S△ABD:S△ACD=($\frac{1}{2}$×AB×DE):($\frac{1}{2}$×AC×DF)=$\frac{m}{n}$.
(3)[解]
∵AD=DE,
∴由
(1)知S△ABD:S△EBD=1:1.
∵S△BDE=6,
∴S△ABD=6.
∵AC=2,AB=4,AD平分∠CAB,
∴由
(2)知S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=S△ACD+S△ABD=3+6=9.
查看更多完整答案,请扫码查看


