《2025年初中必刷题八年级数学上册沪科版》

如图,在$\triangle ACD$中,$\angle CAD= 90^{\circ}$,$AC= 6$,$AD= 8$,$AB// CD$,$E是CD$上一点,$BE与AD相交于点F$,当$AB+CE= CD$时,图中阴影部分的面积为(A)
A.24
B.36
C.48
D.60

答案： A　[解析]AB//CD→∠B=∠BED，∠DAB=∠D；AB+CE=CD，CD=DE+CE→AB=DE；ASA→△ABF≌△DEF；S△ABF=S△DEF；S阴影=S△ACD=$\frac{1}{2}$AC·AD=$\frac{1}{2}$×6×8=24

2 [2025安徽芜湖质检,较难]如图,动点$C与线段AB构成\triangle ABC$,$AB= 9$,$CA= 2a+2$,$CB= 2a-3$。点$D在\angle ACB$的平分线上,且$\angle ADC= 90^{\circ}$,则$a$的取值范围是____,$\triangle ABD$的面积的最大值为____。

答案：
a＞2.5　$\frac{45}{4}$　[解析]
∵AB=9，CA=2a+2，CB=2a−3，满足三角形三边关系定理，
∴2a+2+9＞2a−3，① 2a−3+9＞2a+2，② 2a+2+2a−3＞9，③ 不等式①②显然成立，由③得a＞2.5.如图，延长AD交CB延长线于M，过M作MH⊥AB交AB延长线于H.
∵CD平分∠ACB，
∴∠MCD=∠ACD.
∵∠ADC=90°，
∴∠CDM=180°−90°=90°，
∴∠ADC=∠MDC.又
∵CD=CD，∠MCD=∠ACD，
∴△ACD≌△MCD(ASA)，
∴AD=MD，CM=AC=2a+2，
∴BM=CM−BC=5.
∵AD=MD，
∴S△ABD=$\frac{1}{2}$S△ABM，
∴当△ABM的面积最大时，△ABD的面积最大.
∵△ABM的面积为$\frac{1}{2}$AB·MH，AB=9，MH≤MB=5，
∴△ABD面积的最大值为$\frac{1}{2}$×9×5×$\frac{1}{2}$=$\frac{45}{4}$.
思路分析：由三角形三边关系求出a＞2.5.延长AD交CB延长线于M，过M作MH⊥AB交AB延长线于H，通过证全等推出AD=MD，CM=AC=2a+2，得到BM=CM−BC=5，S△ABD=$\frac{1}{2}$S△ABM，因此当△ABM的面积最大时，△ABD的面积最大，而AB=9，MH≤MB=5，即可求出△ABD的面积的最大值.
关键点拨：由ASA可证△ABF≌△DEF，可得S△ABF=S△DEF，进而可求解.

故答案为a＞2.5，$\frac{45}{4}$.

3 [2024安徽芜湖校级期中,中]如图,$\triangle ABC$中,$DB= DC$,$CD\perp AB于D$,$BE平分\angle ABC$,且$BE\perp AC于E$,与$CD相交于点F$,$H是BC$边的中点,连接$DH交BE于点G$。
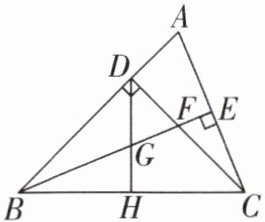
(1)求证：$\triangle BDF\cong\triangle CDA$；
(2)求证：$CE= \frac{1}{2}BF$。

答案： 【证明】
(1)
∵CD⊥AB，BE⊥AC，
∴∠BDF=∠ADC=∠FEC=90°.
∵∠DBF=90°−∠BFD，∠DCA=90°−∠EFC，且∠BFD=∠EFC，
∴∠DBF=∠DCA.在△DFB和△DAC中，∠BDF=∠ADC，BD=CD，∠DBF=∠ACD，
∴△DFB≌△DAC(ASA).
(2)
∵BE平分∠ABC，
∴∠ABE=∠CBE.在△BEA和△BEC中，∠AEB=∠CEB，BE=BE，∠ABE=∠CBE，
∴△BEA≌△BEC(ASA)，
∴CE=AE=$\frac{1}{2}$AC.由
(1)知△DFB≌△DAC，
∴BF=AC，
∴CE=$\frac{1}{2}$AC=$\frac{1}{2}$BF.

4 [2025安徽阜阳颖泉区校级期末,中]在$\triangle ABC$中,$AC= BC$,$\angle ACB= 90^{\circ}$,点$D在BC$的延长线上,$M是BD$的中点,$E是射线CA$上一动点,且$CE= CD$,连接$AD$,作$DF\perp AD$,$DF交EM延长线于点F$。
(1)如图(1),当点$E在CA$上时,$AD$____$DF$(填“=”“＜”或“＞”)。
(2)如图(2),当点$E在CA$的延长线上时,请根据题意将图形补全,判断$AD与DF$的数量关系,并证明你的结论。

答案：
【解】
(1)连接BE，如图
(1)所示.
∵∠ACB=90°，
∴∠DCA=90°.在△ACD和△BCE中，CD=CE，∠DCA=∠ECB，AC=BC，
∴△ACD≌△BCE(SAS)，
∴AD=BE，∠EBM=∠DAC.
∵∠DAC+∠ADC=90°，∠FDM+∠ADC=90°，
∴∠DAC=∠FDM，
∴∠EBM=∠FDM.
∵M是BD的中点，
∴BM=DM.在△EBM和△FDM中，∠EBM=∠FDM，BM=DM，∠EMB=∠FMD，
∴△EBM≌△FDM(ASA)，
∴BE=DF，
∴AD=DF，故答案为=.
(2)补全图形如图
(2)所示.AD与DF的数量关系是AD=DF.证明如下：连接BE.
∵∠ACB=90°，点D在BC的延长线上，
∴∠ACD=∠BCE=90°.在△ACD和△BCE中，AC=BC，∠ACD=∠BCE，CD=CE，
∴△ACD≌△BCE(SAS)，
∴AD=BE，∠ADC=∠BEC.
∵∠ACB=90°，DF⊥AD，
∴∠BEC+∠MBE=∠ADC+∠MDF=90°，
∴∠MBE=∠MDF.
∵M是BD的中点，
∴MB=MD.在△BME和△DMF中，∠MBE=∠MDF，MB=MD，∠EMB=∠FMD，
∴△BME≌△DMF(ASA)，
∴BE=DF，
∴AD=DF.

(1)如图(1),过点$C作PQ交AB于P$,交$DE于Q$,求证：$CP= CQ$；
(2)如图(2),若$AB= 4cm$,点$P从点A$出发,沿$A\to B\to A以3cm/s$的速度运动,点$Q从点D$出发,沿$D\to E以1cm/s$的速度运动,$P$,$Q$两点同时出发。当点$P回到点A$时,$P$,$Q$两点同时停止运动。设点$P的运动时间为t\ s$。连接$PQ$,当线段$PQ经过点C$时,$t$的值为1或2。

答案：
(1)【证明】在△ABC和△EDC中，AC=EC，∠ACB=∠ECD，BC=DC，
∴△ABC≌△EDC(SAS)，
∴∠B=∠D.在△DCQ和△BCP中，∠D=∠B，CD=BC，∠DCQ=∠BCP，
∴△DCQ≌△BCP(ASA)，
∴CP=CQ.
(2)1或2　[解析]由
(1)可知，当线段PQ经过点C时，△DCQ≌△BCP，
∴DQ=BP，则4−3t=t或3t−4=t，
∴t=1或2.故答案为1或2.