《2025年初中必刷题八年级数学上册沪科版》

1 老师在画∠AOB 的平分线 OP 时,在边 OA,OB 上分别取 OM = ON,再用直角三角板分别过点 M,N 作 OA,OB 的垂线,交点为 P,画射线 OP,得到 Rt△OMP≌Rt△ONP 的依据是 (D)
A.AAS
B.ASA
C.SAS
D.HL

答案： D　[解析]由题意得∠OMP=∠ONP=90°，在Rt△OMP和Rt△ONP中，{OP=OP,OM=ON}，
∴Rt△OMP≌Rt△ONP(HL)，故选D。

2 如图,AB⊥BC,AD⊥DC,请你添加一个条件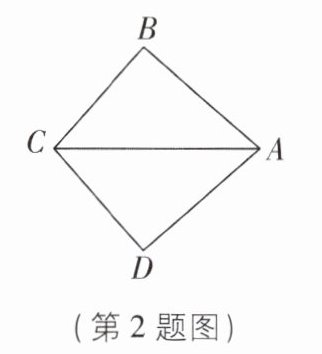AB=AD(或BC=DC),利用“HL”证明 Rt△ABC≌Rt△ADC.

答案： AB=AD(或BC=DC)　[解析]添加AB=AD，理由如下：
∵AB⊥BC，AD⊥DC，
∴∠B=∠D=90°。在Rt△ABC和Rt△ADC中，{AB=AD,AC=AC}，
∴Rt△ABC≌Rt△ADC(HL)。添加BC=DC，同理可证Rt△ABC≌Rt△ADC(HL)。故答案为AB=AD(或BC=DC)。

3 如图,点 E,F 在线段 BD 上,已知 AF⊥BD,CE⊥BD,AD = CB,DE = BF.
求证：△AFD≌△CEB.

答案： [证明]
∵DE=BF，
∴DE+EF=BF+EF，
∴DF=BE。在Rt△AFD和Rt△CEB中，{DF=BE,AD=CB}，
∴Rt△AFD≌Rt△CEB(HL)。

4 [2024 安徽六安期末]下列条件,不能判定两个直角三角形全等的是 (B)
A.斜边和一直角边对应相等
B.两个锐角对应相等
C.一锐角和斜边对应相等
D.两条直角边对应相等

答案： B　[解析]A选项，符合判定定理HL，故本选项正确，不符合题意；B选项，全等三角形的判定必须有边的参与，故本选项错误，符合题意；C选项，符合判定定理AAS，故本选项正确，不符合题意；D选项，符合判定定理SAS，故本选项正确，不符合题意。故选B。

5 [2025 陕西西安期末]如图,MN//PQ,AB⊥PQ,点 A,D 和 B,C 分别在直线 MN 与 PQ 上,点 E 在 AB 上,AD + BC = 7,AD = EB,DE = EC,则 AB = ______.

答案：
7　[解析] 易错警示

6 [2025 安徽铜陵期中]△ABC 和△A'B'C'中,AD 是 BC 边上的高,A'D'是 B'C'边上的高. 若 AD = A'D',AB = A'B',AC = A'C',则∠ACB 与∠A'C'B'的数量关系是______.

答案：
相等或互补　[解析]分两种情况：①当∠A'C'B'为锐角时，如图
(1)所示。
∵AD，A'D'分别为BC，B'C'上的高，
∴AD⊥BC，A'D'⊥B'C'，
∴∠ADC=∠A'D'C'=90°。在Rt△ADC和Rt△A'D'C'中，{AC=A'C',AD=A'D'}，
∴Rt△ADC≌Rt△A'D'C'(HL)，
∴∠C=∠C'。②当∠A'C'B'为钝角时，如图
(2)所示。同①得Rt△ACD≌Rt△A'C'D'(HL)，
∴∠C=∠A'C'D'。
∵∠A'C'B'+∠A'C'D'=180°，
∴∠A'C'B'+∠ACB=180°。综上，∠ACB与∠A'C'B'的数量关系是相等或互补，故答案为相等或互补。

7 [2025 安徽淮南期末]如图,在△ABC 中,∠BAC = 90°,AB = AC,EC⊥AC,垂足为 C,AE 交线段 BC 于 F,D 是 AC 边上一点,连接 BD,且 BD = AE.
(1)求证：CE = AD；
(2)BD 与 AE 有怎样的位置关系？证明你的结论.

答案：
(1)[证明]
∵∠BAC=90°，EC⊥AC，
∴∠ACE=∠BAD=90°。在Rt△ACE和Rt△BAD中，{AE=BD,CA=AB}，
∴Rt△ACE≌Rt△BAD(HL)，
∴CE=AD。
(2)[解]BD⊥AE。证明：设BD与AE交于点O。
∵△ACE≌△BAD，
∴∠CAE=∠ABD，
∴∠AOD=∠BAE+∠ABD=∠BAE+∠CAE=∠BAC=90°，
∴AE⊥BD。

如图,有两个长度相同的滑梯靠在一面墙上. 已知左边滑梯的高度 AC 与右边滑梯的水平长度 DF 相等,那么判定△ABC 与△DEF 全等的依据是HL.

答案： HL　[解析]由题可知∠BAC=∠EDF=90°，
∴在Rt△ABC和Rt△DEF中，{AC=DF,BC=EF}，
∴Rt△ABC≌Rt△DEF(HL)，故答案为HL。