《2025年初中必刷题八年级数学上册沪科版》

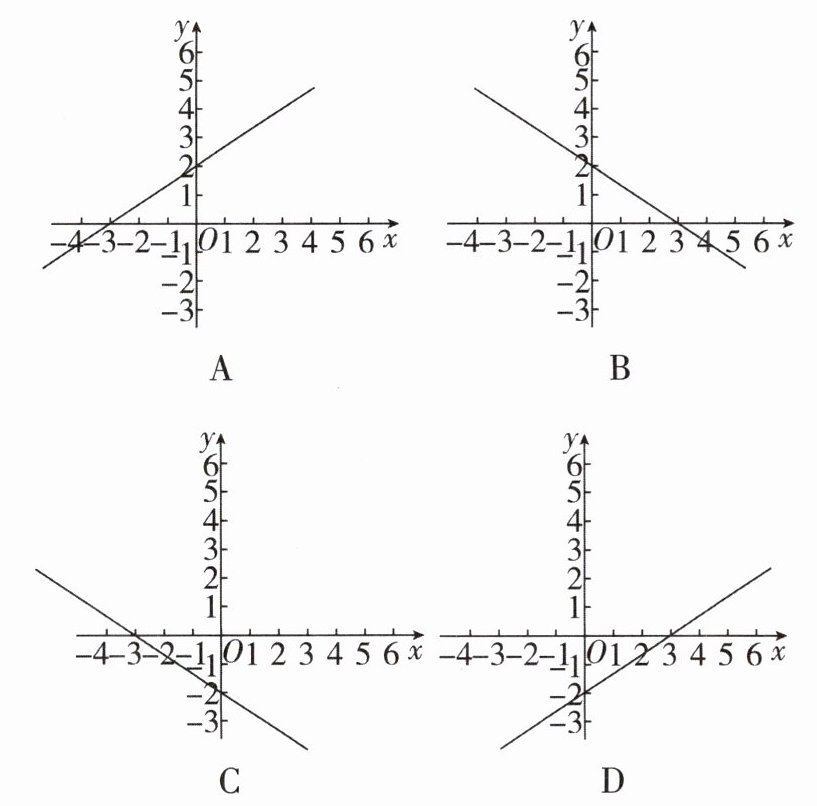
1 [2024 安徽蚌埠期末]下面四条直线,其中直线上的每一个点的坐标都是二元一次方程 $ 2x - 3y = 6 $ 的解的是 (D)

答案： D 【解析】由题意可知二元一次方程2x-3y=6对应的一次函数为$y=\frac{2}{3}x-2$.当x=0时,y=-2;当y=0时,x=3,所以一次函数$y=\frac{2}{3}x-2$的图象与y轴交于点(0,-2),与x轴交于点(3,0),所以选项D符合要求,故选D.

2 若以二元一次方程 $ x + 2y - b = 0 $ 的解为坐标的点 $ (x, y) $ 都在直线 $ y = -\frac{1}{2}x + b - 1 $ 上,则常数 $ b = $2.

答案： 2 【解析】因为以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线$y=-\frac{1}{2}x+b-1$上,直线表达式的等号两边同时乘2得2y=-x+2b-2,变形为x+2y-2b+2=0,所以-b=-2b+2,解得b=2,故答案为2.

3 直线 $ y = -a_1x + b_1 $ 与直线 $ y = a_2x + b_2 $ 有唯一交点,则二元一次方程组 $ \begin{cases} a_1x + y = b_1, \\ a_2x - y = -b_2 \end{cases} $ 的解的情况是 (B)
A.无解
B.有唯一解
C.有两个解
D.有无数解

答案： B 【解析】因为二元一次方程组$\left\{\begin{array}{l} a_{1}x+y=b_{1},\\ a_{2}x-y=-b_{2}\end{array}\right. $的解就是组成二元一次方程组的两个方程的公共解,即直线$y=-a_{1}x+b_{1}$与$y=a_{2}x+b_{2}$的交点坐标,由于两直线的交点唯一,所以方程组的解也唯一.故选B.

4 [2025 安徽亳州蒙城期中]已知关于 $ x, y $ 的二元一次方程组 $ \begin{cases} ax + 1 = y, \\ 2x - b = y \end{cases} $ 的解是 $ \begin{cases} x = \frac{4}{3}, \\ y = \frac{5}{3} \end{cases} $ 直线 $ l_1: y = ax + 1 $ 与直线 $ l_2: y = 2x - b $ 相交于点 $ A $, 若直线 $ y = -2x + m $ 过点 $ A $, 则 $ m $ 的值是____$\frac{13}{3}$.

答案： $\frac{13}{3}$ 【解析】因为关于x,y的二元一次方程组$\left\{\begin{array}{l} ax+1=y,\\ 2x-b=y\end{array}\right. $的解是$\left\{\begin{array}{l} x=\frac{4}{3},\\ y=\frac{5}{3}\end{array}\right. $直线$l_{1}:y=ax+1$与直线$l_{2}:y=2x-b$相交于点A,所以$A\left( \frac{4}{3},\frac{5}{3}\right)$.因为直线$y=-2x+m$过点A,所以$\frac{5}{3}=-2×\frac{4}{3}+m$,解得$m=\frac{13}{3}$.故答案为$\frac{13}{3}$.

5 [2025 重庆沙坪坝区校级质检]已知一次函数 $ y = ax + 2 $ 与 $ y = kx + b $ 的图象如图所示,且方程组 $ \begin{cases} y = ax + 2, \\ y = kx + b \end{cases} $ 的解为 $ \begin{cases} x = 2, \\ y = 1 \end{cases} $ 点 $ B $ 坐标为 $ (0, -1) $, $ y $ 轴上有一个动点 $ P $, 若 $ S_{\triangle ABP} = 4 $, 则点 $ P $ 的坐标为(0,-5)或(0,3).

答案： (0,-5)或(0,3) 【解析】依题意可知,点A的坐标为(2,1),所以$S_{\triangle ABP}=\frac{1}{2}\cdot BP\cdot 2=4$,所以BP=4.因为点P在y轴上,点B坐标为(0,-1),所以点P的坐标为(0,-5)或(0,3),故答案为(0,-5)或(0,3).

若直线 $ l_1: y = ax + b $ ( $ a, b $ 为常数,且 $ a \neq 0 $ ) 与直线 $ l_2: y = mx + n $ ( $ m, n $ 为常数,且 $ m \neq 0 $ ) 的交点坐标为 $ (-2, 1) $, 则直线 $ l_3: y = a(x - 3) + b + 2 $ 与直线 $ l_4: y = m(x - 3) + n + 2 $ 的交点坐标为(1,3).

答案： (1,3) 【解析】由题意可得,a≠m,b≠n,所以a-m≠0,b-n≠0.把(-2,1)分别代入y=ax+b,y=mx+n,得-2a+b=1,-2m+n=1,所以2(a-m)=b-n.联立得$\left\{\begin{array}{l} y=a(x-3)+b+2,\enclose{circle}{1}\\ y=m(x-3)+n+2,\enclose{circle}{2}\end{array}\right. $①-②得(a-m)(x-3)+(b-n)=0,所以x-3=-2,所以x=1.把x=1代入$y=a(x-3)+b+2$得y=-2a+b+2=1+2=3,所以直线$l_{3}:y=a(x-3)+b+2$与直线$l_{4}:y=m(x-3)+n+2$的交点坐标为(1,3).故答案为(1,3).

7 AI DPSK 原创 (1) 借助图象解下列方程组:
① $ \begin{cases} 5x - 2y = 4, \\ 10x - 4y = 8; \end{cases} $
② $ \begin{cases} 3x + 2y = -2, \\ 6x + 4y = 4. \end{cases} $
(2) 平面内两直线 $ l_1 $ 与 $ l_2 $ 可能有怎样的位置关系?
(3) 如果二元一次方程组 $ \begin{cases} a_1x + b_1y = c_1, \\ a_2x + b_2y = c_2 \end{cases} $ ( $ a_1, a_2, b_1, b_2 $ 均不为零) 有唯一的解, $ a_1, a_2, b_1, b_2 $ 应满足怎样的条件?

答案： 【解】
(1)①观察图象可知(图象略),方程组有无数组解.②观察图象可知(图象略)方程组无解.
(2)直线$l_{1}$与$l_{2}$可能平行,可能相交,可能重合.
(3)$\left\{\begin{array}{l} a_{1}x+b_{1}y=c_{1},\\ a_{2}x+b_{2}y=c_{2},\end{array}\right. $变形得$\left\{\begin{array}{l} a_{1}a_{2}x+b_{1}a_{2}y=c_{1}a_{2},\enclose{circle}{1}\\ a_{1}a_{2}x+b_{2}a_{1}y=c_{2}a_{1},\enclose{circle}{2}\end{array}\right.$①-②得$(b_{1}a_{2}-b_{2}a_{1})y=c_{1}a_{2}-c_{2}a_{1}$.因为二元一次方程组$\left\{\begin{array}{l} a_{1}x+b_{1}y=c_{1},\\ a_{2}x+b_{2}y=c_{2}\end{array}\right.(a_{1},a_{2},b_{1},b_{2}$均不为零)有唯一的解,所以$b_{1}a_{2}-b_{2}a_{1}≠0$,所以$\frac{a_{1}}{a_{2}}≠\frac{b_{1}}{b_{2}}$.