《2025年初中必刷题八年级数学上册沪科版》

1 [2025安徽黄山期中,中]如图,在△ABC中,点E,F分别在AC,BC上,EF//AB,∠BCA的平分线交AB于点D,∠MAC是△ABC的外角,若∠MAC= α,∠EFC= β,∠ADC= γ,则α,β,γ三者间的数量关系是(B)
A.β= α+γ
B.β= 2γ-α
C.β= α+2γ
D.β= 2α-2γ

答案： B

如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的平分线BF所在直线与射线AE相交于点G,若∠ABC= 3∠C,且∠G= 20°,则∠DFB的度数为(C)
A.50°
B.55°
C.60°
D.65°

答案： C

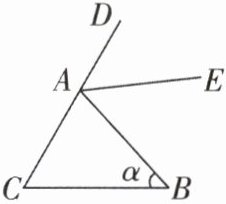
3 [2025辽宁抚顺质检,较难]如图,在△ABC中,∠ACB= 60°,∠ABC= α(20°＜α＜120°),AE平分△ABC的外角∠BAD,CF将∠ACB分成度数之比为1:2的两个角.若AE,CF交于点G,则∠AGC的度数为______$\frac{1}{2}$α+10°或$\frac{1}{2}$α−10°(用含α的代数式表示).

答案： $\frac{1}{2}$α+10°或$\frac{1}{2}$α−10°

(1)若点P在边AB上,如图(1)所示,且∠α= 40°,则∠1+∠2=120°.
(2)若点P在△ABC的外部,如图(2)所示,则∠α,∠1,∠2之间有何关系？说明理由.∠2−∠1=∠α−80°.理由如下:根据三角形外角的性质可知，∠2−∠α=∠1−80°，则∠2−∠1=∠α−80°.
(3)若点P在△ABC边BA的延长线上运动(CE＜CD),求出∠α,∠1,∠2之间的关系.①如图(1),∵∠2=80°+∠3+∠α+∠4,∠1=∠3+∠4,∴∠2=80°+∠α+∠1,则∠2−∠1=∠α+80°.②如图(2),∵∠2=80°+∠3+∠4,∠1=∠3+∠4+∠α,∴∠2−∠1=80°−∠α.综上，∠2−∠1=∠α+80°或∠2−∠1=80°−∠α.

答案： [解]
(1)连接CP.
∵∠1=∠DCP+∠DPC,∠2=∠ECP+∠CPE,
∴∠1+∠2=∠DCP+∠DPC+∠ECP+∠EPC=∠ACB+∠DPE=∠ACB+∠α.
∵∠ACB=80°,∠α=40°,
∴∠1+∠2=80°+40°=120°.故答案为120.
(2)∠2−∠1=∠α−80°.理由如下:根据三角形外角的性质可知，∠2−∠α=∠1−80°，则∠2−∠1=∠α−80°.
(3)①如图
(1),
∵∠2=80°+∠3+∠α+∠4,∠1=∠3+∠4,
∴∠2=80°+∠α+∠1,则∠2−∠1=∠α+80°.
②如图
(2),
∵∠2=80°+∠3+∠4,∠1=∠3+∠4+∠α,
∴∠2−∠1=80°−∠α.
综上，∠2−∠1=∠α+80°或∠2−∠1=80°−∠α.

5 核心素养推理能力[难]已知△ABC中,∠ABC= ∠ACB,D为线段CB上一点(不与C,B重合),点E为射线CA上一点,∠ADE= ∠AED,设∠BAD= α,∠CDE= β.
(1)如图(1),当点E在AC上时,
①若∠BAC= 42°,∠DAE= 30°,则α= 12°,β= 6°.
②若∠BAC= 54°,∠DAE= 36°,则α= 18°,β= 9°.
③写出α与β的数量关系,并说明理由.
α=2β,理由:设∠BAC=x°,∠DAE=y°,则α=x°−y°.∵∠ACB=∠ABC,∴∠ABC=$\frac{180°−x°}{2}$.∵∠ADE=∠AED,∴∠ADE=$\frac{180°−y°}{2}$.∵β+∠ADE=α+∠ABC,∴β+$\frac{180°−y°}{2}$=α+$\frac{180°−x°}{2}$,∴α=2β.
(2)如图(2),当E点在CA的延长线上时,其他条件不变,请直接写出α与β的数量关系.α=2β−180°

答案： [解]
(1)①
∵∠DAE=30°,
∴∠ADE+∠AED=150°,
∴∠ADE=∠AED=75°.
∵∠BAC=42°,
∴α=42°−30°=12°,∠ACB=∠B=$\frac{180°−42°}{2}$=69°.
∵∠ADC=∠B+α,
∴75°+β=69°+12°,
∴β=6°.故答案为12°,6°.
②
∵∠DAE=36°,
∴∠ADE+∠AED=144°,
∴∠ADE=∠AED=72°.
∵∠BAC=54°,
∴α=54°−36°=18°,∠ACB=∠B=$\frac{180°−54°}{2}$=63°.
∵∠ADC=∠B+α,
∴72°+β=63°+18°,
∴β=9°.故答案为18°,9°.
③α=2β,理由:设∠BAC=x°,∠DAE=y°,则α=x°−y°.
∵∠ACB=∠ABC,
∴∠ABC=$\frac{180°−x°}{2}$.
∵∠ADE=∠AED,
∴∠ADE=$\frac{180°−y°}{2}$.
∵β+∠ADE=α+∠ABC,
∴β+$\frac{180°−y°}{2}$=α+$\frac{180°−x°}{2}$,
∴α=2β.
(2)α=2β−180°.设∠E=x°,则∠DAC=2x°,
∴∠BAC=∠BAD+∠DAC=α+2x°,
∴∠B=∠ACB=$\frac{180°−α−2x°}{2}$.
∵∠ADC=∠B+∠BAD,
∴β−x°=$\frac{180°−α−2x°}{2}$+α,
∴α=2β−180°.