第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
12 在△ABC 中,∠B = 40°,∠C = 30°,点 D 在 BC 边上,连接 AD,若△ACD 为直角三角形,则∠BAD 的度数为____.
答案:
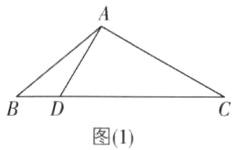
50°或20° [解析]如图
(1),当∠DAC = 90°时,
∵∠C = 30°,
∴∠ADC = 90° - 30° = 60°.
∵∠B = 40°,
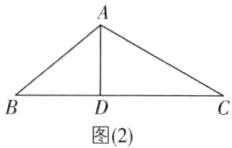
∴∠BAD = 60° - 40° = 20°.如图
(2),当∠ADC = 90°时,
∵∠B = 40°,
∴∠BAD = ∠ADC - ∠B = 90° - 40° = 50°.
故答案为50°或20°.
50°或20° [解析]如图
(1),当∠DAC = 90°时,
∵∠C = 30°,
∴∠ADC = 90° - 30° = 60°.
∵∠B = 40°,
∴∠BAD = 60° - 40° = 20°.如图
(2),当∠ADC = 90°时,
∵∠B = 40°,
∴∠BAD = ∠ADC - ∠B = 90° - 40° = 50°.


故答案为50°或20°.
13 [2025 安徽芜湖期中]如图,D 是△ABC 内一点,连接 AD,BD,CD,P 是∠BDC 的平分线的反向延长线上一点,连接 BP,∠ABP = 2∠PBD,△ABC 和△ACD 的外角平分线相交于点 Q,若∠Q = 45°,∠BDC = 4∠ABD,则∠P 的度数为____°.
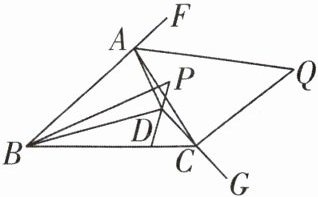

答案:
50 [解析]如图,延长AD交BC于K,设PD的延长线交BC于E.
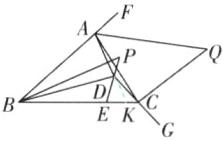
设∠PBD = α,则∠ABP = 2α,
∴∠ABD = ∠ABP + ∠PBD = 3α,
∴∠BDC = 4∠ABD = 12α.
∵DE平分∠BDC,
∴∠BDE = 1/2∠BDC = 6α,
∴∠P = ∠BDE - ∠PBD = 6α - α = 5α.在△ACQ中,∠QAC + ∠ACQ = 180° - ∠Q = 135°.
∵AQ平分∠FAC,CQ平分∠ACG,
∴∠FAC = 2∠QAC,∠ACG = 2∠ACQ,
∴∠FAC + ∠ACG = 2(∠QAC + ∠ACQ) = 270°,
∴∠BAC + ∠ACD = 180° - ∠FAC + 180° - ∠ACG = 90°.
∵∠BDC = ∠BDK + ∠CDK = ∠ABD + ∠BAD + ∠CAD + ∠ACD = ∠ABD + ∠BAC + ∠ACD,
∴12α = 3α + 90°,
∴α = 10°,
∴∠P = 5α = 50°,故答案为50.
50 [解析]如图,延长AD交BC于K,设PD的延长线交BC于E.

设∠PBD = α,则∠ABP = 2α,
∴∠ABD = ∠ABP + ∠PBD = 3α,
∴∠BDC = 4∠ABD = 12α.
∵DE平分∠BDC,
∴∠BDE = 1/2∠BDC = 6α,
∴∠P = ∠BDE - ∠PBD = 6α - α = 5α.在△ACQ中,∠QAC + ∠ACQ = 180° - ∠Q = 135°.
∵AQ平分∠FAC,CQ平分∠ACG,
∴∠FAC = 2∠QAC,∠ACG = 2∠ACQ,
∴∠FAC + ∠ACG = 2(∠QAC + ∠ACQ) = 270°,
∴∠BAC + ∠ACD = 180° - ∠FAC + 180° - ∠ACG = 90°.
∵∠BDC = ∠BDK + ∠CDK = ∠ABD + ∠BAD + ∠CAD + ∠ACD = ∠ABD + ∠BAC + ∠ACD,
∴12α = 3α + 90°,
∴α = 10°,
∴∠P = 5α = 50°,故答案为50.
14 [2025 吉林长春期末]图(1)、图(2)、图(3)均是 4×4 的正方形网格,每个小正方形的边长均为 1,小正方形的顶点称为格点,线段 AB 的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以 AB 为边画△ABC.
要求:
(1)在图(1)中画一个直角三角形,在图(2)中画一个锐角三角形,在图(3)中画一个钝角三角形.
(2)点 C 在格点上.

要求:
(1)在图(1)中画一个直角三角形,在图(2)中画一个锐角三角形,在图(3)中画一个钝角三角形.
(2)点 C 在格点上.

答案:
【解析】:
本题主要考查网格中按要求画三角形,需要根据直角三角形、锐角三角形、钝角三角形的性质,结合网格特点来确定点$C$的位置。
对于直角三角形,可利用网格中垂直的线段来确定直角;对于锐角三角形,要保证三个角都小于$90^{\circ}$;对于钝角三角形,要保证有一个角大于$90^{\circ}$。
【答案】:
(1)
图(1):在图
(1)中,取格点$C$,使得$AC\perp AB$,此时$\triangle ABC$是直角三角形。因为网格中相邻的垂直线段构成直角,通过观察网格特点可找到满足垂直条件的点$C$。
图(2):在图
(2)中,取格点$C$,使得$\triangle ABC$的三个角都小于$90^{\circ}$,构成锐角三角形。可以通过尝试不同的格点,利用勾股定理等知识判断三角形的角的类型。
图(3):在图
(3)中,取格点$C$,使得$\triangle ABC$有一个角大于$90^{\circ}$,构成钝角三角形。同样通过尝试不同格点,结合三角形内角和等知识来确定。
图略。
本题主要考查网格中按要求画三角形,需要根据直角三角形、锐角三角形、钝角三角形的性质,结合网格特点来确定点$C$的位置。
对于直角三角形,可利用网格中垂直的线段来确定直角;对于锐角三角形,要保证三个角都小于$90^{\circ}$;对于钝角三角形,要保证有一个角大于$90^{\circ}$。
【答案】:
(1)
图(1):在图
(1)中,取格点$C$,使得$AC\perp AB$,此时$\triangle ABC$是直角三角形。因为网格中相邻的垂直线段构成直角,通过观察网格特点可找到满足垂直条件的点$C$。
图(2):在图
(2)中,取格点$C$,使得$\triangle ABC$的三个角都小于$90^{\circ}$,构成锐角三角形。可以通过尝试不同的格点,利用勾股定理等知识判断三角形的角的类型。
图(3):在图
(3)中,取格点$C$,使得$\triangle ABC$有一个角大于$90^{\circ}$,构成钝角三角形。同样通过尝试不同格点,结合三角形内角和等知识来确定。
图略。
15 [2024 安徽六安金安区校级期中]概念学习:
已知△ABC,点 P 为其内部一点(包括△ABC 的三边),连接 PA,PB,PC,在△PAB,△PBC 和△PAC 中,如果存在一个三角形,其内角与△ABC 的三个内角分别相等,那么就称点 P 为△ABC 的等角点.
理解应用:
(1)判断以下两个命题是否为真命题,若为真命题,则在相应横线内写“真命题”;反之,则写“假命题”.
①内角分别为 30°,60°,90°的三角形存在等角点:____;
②任意的三角形都存在等角点:____.
(2)如图,点 P 是锐角三角形 ABC 的等角点,若∠BAC = ∠PBC,探究图中∠BPC,∠ABC,∠ACP 之间的数量关系,并说明理由.
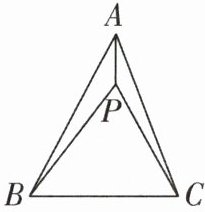
已知△ABC,点 P 为其内部一点(包括△ABC 的三边),连接 PA,PB,PC,在△PAB,△PBC 和△PAC 中,如果存在一个三角形,其内角与△ABC 的三个内角分别相等,那么就称点 P 为△ABC 的等角点.
理解应用:
(1)判断以下两个命题是否为真命题,若为真命题,则在相应横线内写“真命题”;反之,则写“假命题”.
①内角分别为 30°,60°,90°的三角形存在等角点:____;
②任意的三角形都存在等角点:____.
(2)如图,点 P 是锐角三角形 ABC 的等角点,若∠BAC = ∠PBC,探究图中∠BPC,∠ABC,∠ACP 之间的数量关系,并说明理由.

答案:
(1)①真命题;②假命题;
(2)∠BPC = ∠ABC + ∠ACP.理由如下:如图,延长BP交AC于D.
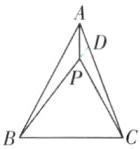
∵∠BPC是△CPD的外角,
∴∠BPC = ∠CDP + ∠ACP.
∵∠CDP = ∠ABP + ∠BAC,
∴∠BPC = ∠ABP + ∠BAC + ∠ACP.
∵∠BAC = ∠PBC,
∴∠BPC = ∠ABP + ∠PBC + ∠ACP = ∠ABC + ∠ACP.
(1)①真命题;②假命题;
(2)∠BPC = ∠ABC + ∠ACP.理由如下:如图,延长BP交AC于D.

∵∠BPC是△CPD的外角,
∴∠BPC = ∠CDP + ∠ACP.
∵∠CDP = ∠ABP + ∠BAC,
∴∠BPC = ∠ABP + ∠BAC + ∠ACP.
∵∠BAC = ∠PBC,
∴∠BPC = ∠ABP + ∠PBC + ∠ACP = ∠ABC + ∠ACP.
16 已知△ABC 的面积是 60,请完成下列问题:
(1)如图(1),若 AD 是△ABC 的 BC 边上的中线,则△ABD 的面积
(2)如图(2),若 CD,BE 分别是△ABC 的 AB,AC 边上的中线,BE 与 CD 交于点 O,求四边形 ADOE 的面积可以用如下方法:连接 AO,由 AD = DB,得 S_{△ADO} = S_{△BDO},同理,S_{△CEO} = S_{△AEO}.设 S_{△BDO} = x,S_{△CEO} = y,则 S_{△ADO} = x,S_{△AEO} = y.由题意得 S_{△ABE} = $\frac{1}{2}$S_{△ABC} = 30,S_{△ADC} = $\frac{1}{2}$S_{△ABC} = 30,故可列方程组 $\begin{cases}2x + y = 30,\\x + 2y = 30,\end{cases} $ 解得
(3)如图(3),已知 AD:DB = 1:3,CE:AE = 1:2,请你计算四边形 ADOE 的面积.
(1)如图(1),若 AD 是△ABC 的 BC 边上的中线,则△ABD 的面积
=
△ACD 的面积(填“>”“<”或“= ”);(2)如图(2),若 CD,BE 分别是△ABC 的 AB,AC 边上的中线,BE 与 CD 交于点 O,求四边形 ADOE 的面积可以用如下方法:连接 AO,由 AD = DB,得 S_{△ADO} = S_{△BDO},同理,S_{△CEO} = S_{△AEO}.设 S_{△BDO} = x,S_{△CEO} = y,则 S_{△ADO} = x,S_{△AEO} = y.由题意得 S_{△ABE} = $\frac{1}{2}$S_{△ABC} = 30,S_{△ADC} = $\frac{1}{2}$S_{△ABC} = 30,故可列方程组 $\begin{cases}2x + y = 30,\\x + 2y = 30,\end{cases} $ 解得
x = 10,y = 10
,从而得到四边形 ADOE 的面积为20
;(3)如图(3),已知 AD:DB = 1:3,CE:AE = 1:2,请你计算四边形 ADOE 的面积.
13
答案:
(1)=;
(2)x = 10,y = 10;20;
(3)13.
(1)=;
(2)x = 10,y = 10;20;
(3)13.
查看更多完整答案,请扫码查看


