第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
在函数 $ y = \sqrt{x - 3} $ 中,自变量 $ x $ 的取值范围是(
A.$ x \neq 3 $
B.$ x > 3 $
C.$ x < 3 $
D.$ x \geq 3 $
D
)A.$ x \neq 3 $
B.$ x > 3 $
C.$ x < 3 $
D.$ x \geq 3 $
答案:
D 【解析】由题意得x - 3≥0,解得x≥3,故选D。
2 新考向 传统文化 [2024 甘肃武威中考]如图(1),“燕几”即宴几,是世界上最早的一套组合桌,由北宋进士黄伯思设计. 全套“燕几”一共有七张桌子,包括两张长桌、两张中桌和三张小桌,每张桌面的宽都相等. 七张桌面分开可组合成不同的图形. 如图(2)给出了《燕几图》中名称为“回文”的桌面拼合方式,若设每张桌面的宽为 $ x $ 尺,长桌的长为 $ y $ 尺,则 $ y $ 与 $ x $ 的关系可以表示为(
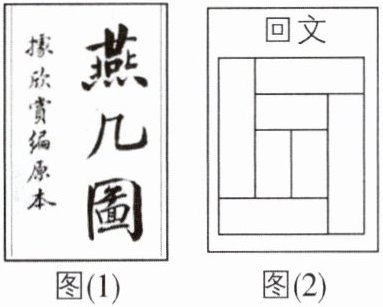
A.$ y = 3x $
B.$ y = 4x $
C.$ y = 3x + 1 $
D.$ y = 4x + 1 $
B
)
A.$ y = 3x $
B.$ y = 4x $
C.$ y = 3x + 1 $
D.$ y = 4x + 1 $
答案:
B 【解析】由题图可知,小桌的长为2x尺,则由题图得到小桌长与宽的数量关系,从而得到长桌长与宽的数量关系是解题的关键。y = x + x + 2x,即y = 4x。故选B。
已知点 $ A(x_1, y_1) $,$ B(x_2, y_2) $ 都在正比例函数 $ y = 3x $ 的图象上,若 $ x_1 < x_2 $,则 $ y_1 $ 与 $ y_2 $ 的大小关系是(
A.$ y_1 > y_2 $
B.$ y_1 < y_2 $
C.$ y_1 = y_2 $
D.$ y_1 \geq y_2 $
B
)A.$ y_1 > y_2 $
B.$ y_1 < y_2 $
C.$ y_1 = y_2 $
D.$ y_1 \geq y_2 $
答案:
B 【解析】因为正比例函数y = 3x中,k = 3>0,所以该函数的函数值y随着x的增大而增大.因为x₁<x₂,所以y₁<y₂。故选B。
4 [2024 内蒙古呼伦贝尔中考]点 $ P(x, y) $ 在直线 $ y = -\frac{3}{4}x + 4 $ 上,坐标 $ (x, y) $ 是二元一次方程 $ 5x - 6y = 33 $ 的解,则点 $ P $ 的位置在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
【解析】:
本题主要考查了一次函数图像上点的坐标特征以及二元一次方程组的解与坐标。
首先,由于点$P(x, y)$在直线$y = -\frac{3}{4}x + 4$上,可以得到一个方程:
$y = -\frac{3}{4}x + 4$,
其次,点$P(x, y)$的坐标是二元一次方程$5x - 6y = 33$的解,因此又得到一个方程:
$5x - 6y = 33$,
现在,我们有一个方程组:
$\begin{cases}y = -\frac{3}{4}x + 4 \\5x - 6y = 33\end{cases}$,
将第一个方程代入第二个方程中,得:
$5x - 6(-\frac{3}{4}x + 4) = 33$,
去括号得:
$5x + \frac{18}{4}x - 24 = 33$,
移项、合并同类项得:
$\frac{20}{4}x + \frac{18}{4}x = 57$,
$\frac{38}{4}x = 57$,
系数化为$1$得:
$x = 6$,
将$x = 6$代入第一个方程得:
$y = -\frac{3}{4} × 6 + 4 = -\frac{1}{2}$,
因此,点$P$的坐标为$(6, -\frac{1}{2})$。
根据坐标系的定义,横坐标大于0,纵坐标小于0的点位于第四象限。
【答案】:D
本题主要考查了一次函数图像上点的坐标特征以及二元一次方程组的解与坐标。
首先,由于点$P(x, y)$在直线$y = -\frac{3}{4}x + 4$上,可以得到一个方程:
$y = -\frac{3}{4}x + 4$,
其次,点$P(x, y)$的坐标是二元一次方程$5x - 6y = 33$的解,因此又得到一个方程:
$5x - 6y = 33$,
现在,我们有一个方程组:
$\begin{cases}y = -\frac{3}{4}x + 4 \\5x - 6y = 33\end{cases}$,
将第一个方程代入第二个方程中,得:
$5x - 6(-\frac{3}{4}x + 4) = 33$,
去括号得:
$5x + \frac{18}{4}x - 24 = 33$,
移项、合并同类项得:
$\frac{20}{4}x + \frac{18}{4}x = 57$,
$\frac{38}{4}x = 57$,
系数化为$1$得:
$x = 6$,
将$x = 6$代入第一个方程得:
$y = -\frac{3}{4} × 6 + 4 = -\frac{1}{2}$,
因此,点$P$的坐标为$(6, -\frac{1}{2})$。
根据坐标系的定义,横坐标大于0,纵坐标小于0的点位于第四象限。
【答案】:D
如图,在同一平面直角坐标系中,一次函数 $ y = k_1x + b_1 $ 与 $ y = k_2x + b_2 $(其中 $ k_1k_2 \neq 0 $,$ k_1 $,$ k_2 $,$ b_1 $,$ b_2 $ 为常数)的图象分别为直线 $ l_1 $,$ l_2 $. 下列结论正确的是(
A.$ b_1 + b_2 > 0 $
B.$ b_1b_2 > 0 $
C.$ k_1 + k_2 < 0 $
D.$ k_1k_2 < 0 $
A
)A.$ b_1 + b_2 > 0 $
B.$ b_1b_2 > 0 $
C.$ k_1 + k_2 < 0 $
D.$ k_1k_2 < 0 $
答案:
A 【解析】由图象可得,b₁ = 2,b₂ = -1,k₁>0,k₂>0,所以b₁ + b₂>0,故选项A正确,符合题意;b₁b₂<0,故选项B错误,不符合题意;k₁ + k₂>0,故选项C错误,不符合题意;k₁k₂>0,故选项D错误,不符合题意。故选A。
6 新考向 开放性试题 [2024 内蒙古包头中考]在平面直角坐标系中,若一次函数的图象经过第一、二、三象限,请写出一个符合该条件的一次函数的表达式
y = x + 1(答案不唯一)
.
答案:
y = x + 1(答案不唯一) 【解析】设一次函数的表达式为y = kx + b(k≠0)。因为一次函数的图象经过第一、二、三象限,所以k>0,b>0,则一次函数的表达式可以是y = x + 1。故答案为y = x + 1(答案不唯一)。
7 [2024 西藏中考]将正比例函数 $ y = 2x $ 的图象向上平移 3 个单位长度后得到函数图象的表达式为
y = 2x + 3
.
答案:
y = 2x + 3 【解析】将正比例函数y = 2x的图象向上平移3个单位长度后得到函数图象的表达式为y = 2x + 3。故答案为y = 2x + 3。
8 [2024 江苏扬州中考]如图,已知一次函数 $ y = kx + b $($ k \neq 0 $)的图象分别与 $ x $,$ y $ 轴交于 $ A $,$ B $ 两点,若 $ OA = 2 $,$ OB = 1 $,则关于 $ x $ 的方程 $ kx + b = 0 $ 的解为

x = -2
.
答案:
x = -2 【解析】因为一次函数y = kx + b(k≠0)的图象与x轴交于点A,且OA = 2,所以A(-2,0),所以关于x的方程kx + b = 0的解为x = -2,故答案为x = -2。
9 [2024 江苏南通中考]平面直角坐标系 $ xOy $ 中,已知 $ A(3, 0) $,$ B(0, 3) $. 直线 $ y = kx + b $($ k $,$ b $ 为常数,且 $ k > 0 $)经过点 $ (1, 0) $,并把 $ \triangle AOB $ 分成两部分,其中靠近原点部分的面积为 $ \frac{15}{4} $,则 $ k $ 的值为______.
答案:
3/5 【解析】如图,设AB与直线y = kx + b交于点P。 设AB所在直线的函数表达式为y = k₁x + b₁(k₁,b₁为常数,且k₁≠0)。将A(3,0)和B(0,3)分别代入y = k₁x + b₁,得{3k₁ + b₁ = 0,b₁ = 3},解得{k₁ = -1, b₁ = 3},所以AB所在直线的函数表达式为y = -x + 3。将点(1,0)代入y = kx + b,得k + b = 0,所以b = -k,所以y = kx + b为y = kx - k。联立{y = kx - k,y = -x + 3},解得{x = (k + 3)/(k + l),y = 2k/(k + 1)},所以P((k + 3)/(k + 1),2k/(k + 1))。因为S△AOB = 1/2×3×3 = 9/2,所以远离原点部分的面积为9/2 - 15/4 = 3/4,所以1/2×(3 - 1)×|2k/(k + 1)| = 3/4,所以k = 3/5。故答案为3/5。
设AB所在直线的函数表达式为y = k₁x + b₁(k₁,b₁为常数,且k₁≠0)。将A(3,0)和B(0,3)分别代入y = k₁x + b₁,得{3k₁ + b₁ = 0,b₁ = 3},解得{k₁ = -1, b₁ = 3},所以AB所在直线的函数表达式为y = -x + 3。将点(1,0)代入y = kx + b,得k + b = 0,所以b = -k,所以y = kx + b为y = kx - k。联立{y = kx - k,y = -x + 3},解得{x = (k + 3)/(k + l),y = 2k/(k + 1)},所以P((k + 3)/(k + 1),2k/(k + 1))。因为S△AOB = 1/2×3×3 = 9/2,所以远离原点部分的面积为9/2 - 15/4 = 3/4,所以1/2×(3 - 1)×|2k/(k + 1)| = 3/4,所以k = 3/5。故答案为3/5。
3/5 【解析】如图,设AB与直线y = kx + b交于点P。
 设AB所在直线的函数表达式为y = k₁x + b₁(k₁,b₁为常数,且k₁≠0)。将A(3,0)和B(0,3)分别代入y = k₁x + b₁,得{3k₁ + b₁ = 0,b₁ = 3},解得{k₁ = -1, b₁ = 3},所以AB所在直线的函数表达式为y = -x + 3。将点(1,0)代入y = kx + b,得k + b = 0,所以b = -k,所以y = kx + b为y = kx - k。联立{y = kx - k,y = -x + 3},解得{x = (k + 3)/(k + l),y = 2k/(k + 1)},所以P((k + 3)/(k + 1),2k/(k + 1))。因为S△AOB = 1/2×3×3 = 9/2,所以远离原点部分的面积为9/2 - 15/4 = 3/4,所以1/2×(3 - 1)×|2k/(k + 1)| = 3/4,所以k = 3/5。故答案为3/5。
设AB所在直线的函数表达式为y = k₁x + b₁(k₁,b₁为常数,且k₁≠0)。将A(3,0)和B(0,3)分别代入y = k₁x + b₁,得{3k₁ + b₁ = 0,b₁ = 3},解得{k₁ = -1, b₁ = 3},所以AB所在直线的函数表达式为y = -x + 3。将点(1,0)代入y = kx + b,得k + b = 0,所以b = -k,所以y = kx + b为y = kx - k。联立{y = kx - k,y = -x + 3},解得{x = (k + 3)/(k + l),y = 2k/(k + 1)},所以P((k + 3)/(k + 1),2k/(k + 1))。因为S△AOB = 1/2×3×3 = 9/2,所以远离原点部分的面积为9/2 - 15/4 = 3/4,所以1/2×(3 - 1)×|2k/(k + 1)| = 3/4,所以k = 3/5。故答案为3/5。 10 [2024 北京中考]在平面直角坐标系 $ xOy $ 中,函数 $ y = kx + b $($ k \neq 0 $)与 $ y = -kx + 3 $ 的图象交于点 $ (2, 1) $.
(1) 求 $ k $,$ b $ 的值;
(2) 当 $ x > 2 $ 时,对于 $ x $ 的每一个值,函数 $ y = mx $($ m \neq 0 $)的值既大于函数 $ y = kx + b $ 的值,也大于函数 $ y = -kx + 3 $ 的值,直接写出 $ m $ 的取值范围.
(1) 求 $ k $,$ b $ 的值;
(2) 当 $ x > 2 $ 时,对于 $ x $ 的每一个值,函数 $ y = mx $($ m \neq 0 $)的值既大于函数 $ y = kx + b $ 的值,也大于函数 $ y = -kx + 3 $ 的值,直接写出 $ m $ 的取值范围.
答案:
(1)将(2,1)代入y = -kx + 3,得-2k + 3 = 1,解得k = 1。将(2,1)代入y = x + b中,得2 + b = 1,解得b = -1。
(2)m≥1。因为k = 1,b = -1,所以两个一次函数的表达式分别为y = x - 1,y = -x + 3。当x>2时,对于x的每一个值,函数y = mx(m≠0)的值既大于函数y = kx + b的值,也大于函数y = -kx + 3的值,即当x>2时,直线y = mx(m≠0)在直线y = x - 1和直线y = -x + 3的上方,画出图象如下:
 由图象得当直线y = mx(m≠0)与直线y = x - 1平行时,如图
由图象得当直线y = mx(m≠0)与直线y = x - 1平行时,如图
(1),符合题意,此时m = 1;当y = mx(m≠0)与x轴的夹角大于直线y = mx(m≠0)与直线y = x - 1平行时与x轴的夹角时,如图
(2),也符合题意,此时m>1,所以m的取值范围为m≥1。
(1)将(2,1)代入y = -kx + 3,得-2k + 3 = 1,解得k = 1。将(2,1)代入y = x + b中,得2 + b = 1,解得b = -1。
(2)m≥1。因为k = 1,b = -1,所以两个一次函数的表达式分别为y = x - 1,y = -x + 3。当x>2时,对于x的每一个值,函数y = mx(m≠0)的值既大于函数y = kx + b的值,也大于函数y = -kx + 3的值,即当x>2时,直线y = mx(m≠0)在直线y = x - 1和直线y = -x + 3的上方,画出图象如下:

 由图象得当直线y = mx(m≠0)与直线y = x - 1平行时,如图
由图象得当直线y = mx(m≠0)与直线y = x - 1平行时,如图(1),符合题意,此时m = 1;当y = mx(m≠0)与x轴的夹角大于直线y = mx(m≠0)与直线y = x - 1平行时与x轴的夹角时,如图
(2),也符合题意,此时m>1,所以m的取值范围为m≥1。
查看更多完整答案,请扫码查看


