第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2024安徽芜湖期末]有一块三角形玻璃在运输过程中,不小心碎成如图所示的四块,嘉淇想按原来的大小在玻璃店再订制一块,需要带的两块可以是(
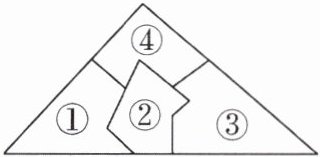
A.①②
B.②③
C.①③
D.①④
D
)
A.①②
B.②③
C.①③
D.①④
答案:
D [解析]想按原来的大小在玻璃店再订制一块,需要带的两块可以是①④或②④或③④,故选D.
2 如图,三角形纸片被遮住了一部分,小明根据所学知识画出了一个与原三角形完全重合的三角形,他画图的依据是(
A.SSS
B.AAS
C.ASA
D.SAS
C
)A.SSS
B.AAS
C.ASA
D.SAS
答案:
C [解析]他画图的依据是ASA,即两角及其夹边对应相等的两个三角形全等,故选C.
3 [2025安徽滁州质检]如图,已知$AB= AC$,当添加条件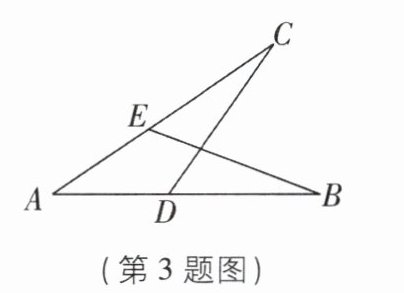
∠B=∠C
时,可由“角边角”判定$\triangle ABE\cong\triangle ACD$。
答案:
∠B=∠C [解析]添加∠B=∠C.在△ABE与△ACD中,∠A=∠A,AB=AC,∠B=∠C,
∴△ABE≌△ACD(ASA),故答案为∠B=∠C.
∴△ABE≌△ACD(ASA),故答案为∠B=∠C.
4 [2025安徽淮南期末]如图,$AC// DF$,点$B为线段AC$上一点,连接$BF交DC于点H$,过点$A作AE// BF分别交DC$,$DF于点G$,$E$,$DG= CH$,求证:$\triangle DFH\cong\triangle CAG$。


答案:
【证明】
∵AC//DF,AE//BF,
∴∠C=∠D,∠AGC=∠DHF.
∵DG=CH,
∴CH+HG=HG+DG,即CG=DH.在△CAG和△DFH中,∠C=∠D,CG=DH,∠AGC=∠DHF,
∴△CAG≌△DFH(ASA).
∵AC//DF,AE//BF,
∴∠C=∠D,∠AGC=∠DHF.
∵DG=CH,
∴CH+HG=HG+DG,即CG=DH.在△CAG和△DFH中,∠C=∠D,CG=DH,∠AGC=∠DHF,
∴△CAG≌△DFH(ASA).
5 如图,$D是AB$延长线上一点,$DF交AC于点E$,$AE= CE$,$FC// AB$,若$AB= 3$,$CF= 5$,则$BD$的长是(
A.0.5
B.1
C.1.5
D.2
D
)A.0.5
B.1
C.1.5
D.2
答案:
D [解析]
∵FC//AB,
∴∠FCE=∠DAE.在△CFE和△ADE中,∠FCE=∠DAE,CE=AE,∠CEF=∠AED,
∴△CFE≌△ADE(ASA),
∴AD=CF=5.
∵AB=3,
∴BD=5−3=2,故选D.
∵FC//AB,
∴∠FCE=∠DAE.在△CFE和△ADE中,∠FCE=∠DAE,CE=AE,∠CEF=∠AED,
∴△CFE≌△ADE(ASA),
∴AD=CF=5.
∵AB=3,
∴BD=5−3=2,故选D.
6 [2025安徽阜阳校级质检]如图,已知$AC= DF且AC$,$DF交于点G$,$\angle A= \angle D$,$\angle ACB= \angle DFE$,$\triangle DEF的面积为25cm^{2}$,四边形$ABFG的面积为21cm^{2}$,若$CF= 2cm$,则$G点到CF$的距离为____
4
cm。
答案:
4 [解析]过点G作GH⊥CF于H.
∵∠A=∠D,AC=DF,∠ACB=∠DFE,
∴△ABC≌△DEF(ASA),
∴S△ABC=S△DEF=25cm²,
∴S△FCG=S△ABC−S四边形ABFG=25−21=4(cm²).
∵CF=2cm,
∴S△FCG=$\frac{1}{2}$CF·GH=$\frac{1}{2}$×2×GH = 4,
∴GH=4cm,则G点到CF的距离为4cm,故答案为4.
∵∠A=∠D,AC=DF,∠ACB=∠DFE,
∴△ABC≌△DEF(ASA),
∴S△ABC=S△DEF=25cm²,
∴S△FCG=S△ABC−S四边形ABFG=25−21=4(cm²).
∵CF=2cm,
∴S△FCG=$\frac{1}{2}$CF·GH=$\frac{1}{2}$×2×GH = 4,
∴GH=4cm,则G点到CF的距离为4cm,故答案为4.
7 [2025安徽合肥期末]如图,在$\triangle ABC$中,$CA= CB$,$\angle ACB= 90^{\circ}$,$D为\triangle ABC$外一点,且$AD\perp BD$,$BD交AC于点E$,$G为BD$上一点,且$\angle BCG= \angle DCA$,过点$G作GH\perp CG交CB于点H$。
(1)求证:$CD= CG$;
(2)若$AD= CG$,求证:$AE= CH$。

(1)求证:$CD= CG$;
(2)若$AD= CG$,求证:$AE= CH$。

答案:
【证明】
(1)
∵AD⊥BD,
∴∠ADB=∠ACB=90°.
∵∠AED=∠BEC,
∴∠CAD=∠CBG.在△ACD和△BCG中,∠DCA=∠BCG,AC=BC,∠CAD=∠CBG,
∴△ACD≌△BCG(ASA),
∴CD=CG.
(2)
∵GH⊥CG,
∴∠CGH=∠ADE=90°.
∵AD=CG,CD=CG,
∴AD=CD,
∴∠DAC=∠DCA,
∴∠BCG=∠DAC.
∵∠CAD=∠GCH,AD=CG,∠ADE=∠CGH,
∴△ADE≌△CGH(ASA),
∴AE=CH.
(1)
∵AD⊥BD,
∴∠ADB=∠ACB=90°.
∵∠AED=∠BEC,
∴∠CAD=∠CBG.在△ACD和△BCG中,∠DCA=∠BCG,AC=BC,∠CAD=∠CBG,
∴△ACD≌△BCG(ASA),
∴CD=CG.
(2)
∵GH⊥CG,
∴∠CGH=∠ADE=90°.
∵AD=CG,CD=CG,
∴AD=CD,
∴∠DAC=∠DCA,
∴∠BCG=∠DAC.
∵∠CAD=∠GCH,AD=CG,∠ADE=∠CGH,
∴△ADE≌△CGH(ASA),
∴AE=CH.
8 如图,要测量水池的宽度$AB$,可从点$A出发在地面上画一条线段AC$,使$AC\perp AB$,再从点$C$观测,在$BA的延长线上取一点D$,使$\angle ACD= \angle ACB$,这时量得$AD= 160m$,则水池宽$AB$是

160
m。
答案:
160 [解析]
∵AC⊥BD,
∴∠CAD=∠CAB=90°.在△ACD和△ACB中,∠DAC=∠BAC,AC=AC,∠ACD=∠ACB,
∴△ACD≌△ACB(ASA),
∴AB=AD=160m.故答案为160.
∵AC⊥BD,
∴∠CAD=∠CAB=90°.在△ACD和△ACB中,∠DAC=∠BAC,AC=AC,∠ACD=∠ACB,
∴△ACD≌△ACB(ASA),
∴AB=AD=160m.故答案为160.
查看更多完整答案,请扫码查看


