第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 如图,已知$∠ACB = 90^{\circ}$,$CD⊥AB$,垂足为 D. 则下列结论中一定正确的是(
A.$∠1 = ∠A$
B.$∠1 + ∠B = 90^{\circ}$
C.$∠2 = ∠A$
D.$∠A = ∠B$
C
)A.$∠1 = ∠A$
B.$∠1 + ∠B = 90^{\circ}$
C.$∠2 = ∠A$
D.$∠A = ∠B$
答案:
C 【解析】
∵∠ACB=90°,CD⊥AB,
∴∠1+∠A=90°,∠1+∠2=90°,∠A+∠B=90°,
∴∠1=∠B,∠2=∠A,
∴A、B、D选项不一定正确,C选项正确.故选C.
∵∠ACB=90°,CD⊥AB,
∴∠1+∠A=90°,∠1+∠2=90°,∠A+∠B=90°,
∴∠1=∠B,∠2=∠A,
∴A、B、D选项不一定正确,C选项正确.故选C.
如图,在$△ABC$中,$∠C = 60^{\circ}$,$∠B = 50^{\circ}$,D 是 BC 上一点,$DE⊥AB$于点 E,$DF⊥AC$于点 F,则$∠EDF$的度数为(
A.$90^{\circ}$
B.$100^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$
C
)A.$90^{\circ}$
B.$100^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$
答案:
C 【解析】
∵在△BED中,∠B=50°,DE⊥AB,
∴∠EDB=40°.
∵在△CDF中,∠C=60°,DF⊥AC,
∴∠FDC=30°,
∴∠EDF=180°−∠EDB−∠FDC=110°.故选C.
∵在△BED中,∠B=50°,DE⊥AB,
∴∠EDB=40°.
∵在△CDF中,∠C=60°,DF⊥AC,
∴∠FDC=30°,
∴∠EDF=180°−∠EDB−∠FDC=110°.故选C.
3 [2024 广东深圳光明区期末] 脊柱侧弯是指脊柱的一个或数个节段向侧方弯曲或伴有椎体旋转的脊柱畸形,医学上常用 Cobb 角来评估脊柱侧弯的程度,当 Cobb 角$>10^{\circ}$时为脊柱侧弯. 如图是脊柱侧弯 Cobb 角$(∠O)$的检测示意图,$DA⊥OC$于 A,$CB⊥OD$于 B,已知 Cobb 角为$37^{\circ}$,则$∠AEC$的大小是(
A.$37^{\circ}$
B.$45^{\circ}$
C.$53^{\circ}$
D.$63^{\circ}$
A
)A.$37^{\circ}$
B.$45^{\circ}$
C.$53^{\circ}$
D.$63^{\circ}$
答案:
A 【解析】
∵DA⊥OC于A,CB⊥OD于B,
∴△DOA和△DBE都是直角三角形,
∴∠O+∠ADO=90°,∠DEB+∠ADO=90°,
∴∠DEB=∠O=37°,
∴∠AEC=∠DEB=37°,故选A.
∵DA⊥OC于A,CB⊥OD于B,
∴△DOA和△DBE都是直角三角形,
∴∠O+∠ADO=90°,∠DEB+∠ADO=90°,
∴∠DEB=∠O=37°,
∴∠AEC=∠DEB=37°,故选A.
如图,在$Rt△ABC$中,$∠ACB = 90^{\circ}$,点 D 在 AB 边上,将$△CBD$沿 CD 折叠,使点 B 恰好落在 AC 边上的点 E 处. 若$∠A = 27^{\circ}$,则$∠CDE = $
72
$^{\circ}$.
答案:
72 【解析】
∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠B=∠CED.
∵∠A=27°,
∴∠B=90°−27°=63°,
∴∠CED=∠B=63°,
∴∠CDE=180°−45°−63°=72°,故答案为72.
∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠B=∠CED.
∵∠A=27°,
∴∠B=90°−27°=63°,
∴∠CED=∠B=63°,
∴∠CDE=180°−45°−63°=72°,故答案为72.
5 如图,小明在计算机上用“几何画板”画了一个$Rt△ABC$,其中$∠C = 90^{\circ}$,并画出了两锐角的平分线 AD,BE 及其交点 F. 小明发现,无论怎样变动$Rt△ABC$的形状和大小,$∠AFB$的度数都是定值,则这个定值为
135°
.
答案:
135° 【解析】
∵∠C=90°,
∴∠CAB+∠CBA=90°.
∵AD平分∠CAB,BE平分∠ABC,
∴∠FAB=$\frac{1}{2}$∠CAB,∠FBA=$\frac{1}{2}$∠CBA,
∴∠FAB+∠FBA=$\frac{1}{2}$(∠CAB+∠CBA)=45°,
∴∠AFB=180°−45°=135°.故答案为135°.
∵∠C=90°,
∴∠CAB+∠CBA=90°.
∵AD平分∠CAB,BE平分∠ABC,
∴∠FAB=$\frac{1}{2}$∠CAB,∠FBA=$\frac{1}{2}$∠CBA,
∴∠FAB+∠FBA=$\frac{1}{2}$(∠CAB+∠CBA)=45°,
∴∠AFB=180°−45°=135°.故答案为135°.
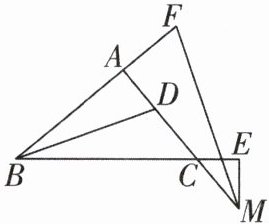
6 [2025 福建泉州丰泽区校级期中] 如图,线段$BA⊥AC$于点 A,BD 平分$∠ABC$,M 为线段 AC 延长线上一点,过 M 作$ME⊥BC$,垂足为 E,$∠AME$的平分线交 BA 延长线于点 F.
(1)证明:$∠ABC = ∠CME$.
(2)你能判断 BD,MF 的位置关系吗?请说明理由.
(1)证明:$∠ABC = ∠CME$.
(2)你能判断 BD,MF 的位置关系吗?请说明理由.

答案:
(1)【证明】
∵BA⊥AC,ME⊥BC,
∴∠BAC=∠MEC=90°,
∴∠ABC+∠ACB=90°,∠ECM+∠CME=90°.
∵∠ACB=∠ECM,
∴∠ABC=∠CME.
(2)【解】BD⊥FM.理由:延长BD交FM于点G,如图.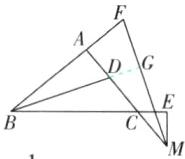
∵BD平分∠ABC,MF平分∠CME,
∴∠ABG=$\frac{1}{2}$∠ABC,∠CMF=$\frac{1}{2}$∠CME.
∵∠ABC=∠CME,
∴∠ABG=∠CMF.
∵BA⊥AC,
∴∠FAM=90°,
∴∠F+∠CMF=90°,
∴∠F+∠ABG=90°,
∴∠BGF=180°-(∠F+∠ABG)=90°,
∴BD⊥FM.
(1)【证明】
∵BA⊥AC,ME⊥BC,
∴∠BAC=∠MEC=90°,
∴∠ABC+∠ACB=90°,∠ECM+∠CME=90°.
∵∠ACB=∠ECM,
∴∠ABC=∠CME.
(2)【解】BD⊥FM.理由:延长BD交FM于点G,如图.

∵BD平分∠ABC,MF平分∠CME,
∴∠ABG=$\frac{1}{2}$∠ABC,∠CMF=$\frac{1}{2}$∠CME.
∵∠ABC=∠CME,
∴∠ABG=∠CMF.
∵BA⊥AC,
∴∠FAM=90°,
∴∠F+∠CMF=90°,
∴∠F+∠ABG=90°,
∴∠BGF=180°-(∠F+∠ABG)=90°,
∴BD⊥FM.
有下列条件:①$∠A + ∠B = ∠C$,②$∠A = 2∠B = 3∠C$,③$∠A:∠B:∠C = 1:2:3$,④$∠A = 90^{\circ} - ∠B$,⑤$∠A = ∠B = \frac{1}{2}∠C$中,其中能确定$△ABC$是直角三角形的条件有(
A.2 个
B.3 个
C.4 个
D.5 个
C
)A.2 个
B.3 个
C.4 个
D.5 个
答案:
C 【解析】①
∵∠A+∠B=∠C,
∴∠A+∠B+∠C=2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故①正确;②
∵∠A=2∠B=3∠C,
∴∠A+∠B+∠C=∠A+$\frac{1}{2}$∠A+$\frac{1}{3}$∠A=180°,
∴∠A=$\frac{1080°}{11}$,
∴△ABC不是直角三角形,故②不正确;③
∵∠A:∠B:∠C=1:2:3,
∴∠C=180°×$\frac{3}{1+2+3}$=90°,
∴△ABC是直角三角形,故③正确;④
∵∠A=90°-∠B,
∴∠A+∠B=90°,
∴∠C=180°-90°=90°,
∴△ABC是直角三角形,故④正确;⑤
∵∠A=∠B=$\frac{1}{2}$∠C,
∴∠A+∠B+∠C=$\frac{1}{2}$∠C+$\frac{1}{2}$∠C+∠C=2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故⑤正确.综上所述,能确定△ABC是直角三角形的条件是①③④⑤,共4个.故选C.
∵∠A+∠B=∠C,
∴∠A+∠B+∠C=2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故①正确;②
∵∠A=2∠B=3∠C,
∴∠A+∠B+∠C=∠A+$\frac{1}{2}$∠A+$\frac{1}{3}$∠A=180°,
∴∠A=$\frac{1080°}{11}$,
∴△ABC不是直角三角形,故②不正确;③
∵∠A:∠B:∠C=1:2:3,
∴∠C=180°×$\frac{3}{1+2+3}$=90°,
∴△ABC是直角三角形,故③正确;④
∵∠A=90°-∠B,
∴∠A+∠B=90°,
∴∠C=180°-90°=90°,
∴△ABC是直角三角形,故④正确;⑤
∵∠A=∠B=$\frac{1}{2}$∠C,
∴∠A+∠B+∠C=$\frac{1}{2}$∠C+$\frac{1}{2}$∠C+∠C=2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故⑤正确.综上所述,能确定△ABC是直角三角形的条件是①③④⑤,共4个.故选C.
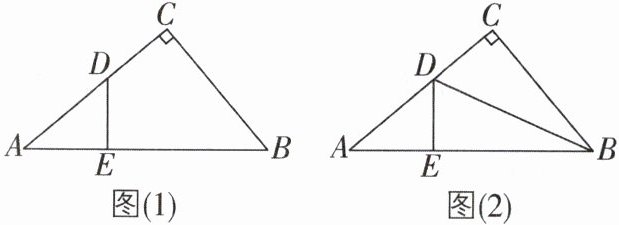
8 [2025 安徽蚌埠蚌山区期中] 在$Rt△ABC$中,$∠C = 90^{\circ}$,点 D,E 分别在 AC,AB 上.
(1)如图(1),若$∠ADE = ∠B$,证明:$△ADE$是直角三角形;
(2)如图(2),连接 BD,若 BD 平分$∠ABC$,$∠A = 40^{\circ}$,求$∠ADB$的度数.
(1)如图(1),若$∠ADE = ∠B$,证明:$△ADE$是直角三角形;
(2)如图(2),连接 BD,若 BD 平分$∠ABC$,$∠A = 40^{\circ}$,求$∠ADB$的度数.

答案:
(1)【证明】
∵∠C=90°,
∴∠A+∠B=90°.
∵∠ADE=∠B,
∴∠A+∠ADE=90°,
∴∠AED=90°,
∴△ADE是直角三角形.
(2)【解】
∵∠C=90°,∠A=40°,
∴∠ABC=180°−∠C−∠A=180°−90°−40°=50°.
∵BD是∠ABC的平分线,
∴∠DBC=$\frac{1}{2}$∠ABC=25°.
∵∠ADB+∠CDB=180°,∠C+∠DBC+∠CDB=180°,
∴∠ADB=∠C+∠DBC=90°+25°=115°.
(1)【证明】
∵∠C=90°,
∴∠A+∠B=90°.
∵∠ADE=∠B,
∴∠A+∠ADE=90°,
∴∠AED=90°,
∴△ADE是直角三角形.
(2)【解】
∵∠C=90°,∠A=40°,
∴∠ABC=180°−∠C−∠A=180°−90°−40°=50°.
∵BD是∠ABC的平分线,
∴∠DBC=$\frac{1}{2}$∠ABC=25°.
∵∠ADB+∠CDB=180°,∠C+∠DBC+∠CDB=180°,
∴∠ADB=∠C+∠DBC=90°+25°=115°.
查看更多完整答案,请扫码查看


