第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2024河北唐山期末,中]如图,△ABC中,∠A= 65°,直线DE交AB于点D,交AC于点E,则∠BDE+∠CED= (
A.180°
B.215°
C.235°
D.245°
D
)A.180°
B.215°
C.235°
D.245°
答案:
D [解析]
∵∠A=65°,
∴∠ADE+∠AED=180°−65°=115°,
∴∠BDE+∠CED=360°−115°=245°,故选D.
∵∠A=65°,
∴∠ADE+∠AED=180°−65°=115°,
∴∠BDE+∠CED=360°−115°=245°,故选D.
如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BCED的外部点A'处时,测得∠1= 70°,∠2= 140°,则∠A的度数为 (
A.25°
B.30°
C.35°
D.40°
B
)A.25°
B.30°
C.35°
D.40°
答案:
B [解析]
∵∠1=70°,∠2=140°,
∴∠B+∠C=360°−∠1−∠2=360°−70°−140°=150°,
∴∠A=180°−(∠B+∠C)=180°−150°=30°.故选B.
∵∠1=70°,∠2=140°,
∴∠B+∠C=360°−∠1−∠2=360°−70°−140°=150°,
∴∠A=180°−(∠B+∠C)=180°−150°=30°.故选B.
3 [2024河北唐山期末,中]如图,∠ABD,∠ACD的平分线交于点P,若∠A= 55°,∠D= 15°,则∠P的度数为 (
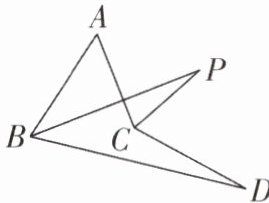
A.15°
B.20°
C.25°
D.30°
B
)
A.15°
B.20°
C.25°
D.30°
答案:
B [解析]如图,延长PC交BD于E.
∵∠ABD,∠ACD的平分线交于点P,
∴∠1=∠2,∠3=∠4.由三角形的内角和定理得,∠A+∠1=∠P+∠3.①在△PBE中,∠5=∠2+∠P,在△DCE中,∠5=∠4−∠D,
∴∠2+∠P=∠4−∠D.②①−②得∠A−∠P=∠P+∠D,
∴∠P=$\frac{1}{2}$(∠A−∠D).
∵∠A=55°,∠D=15°,
∴∠P=$\frac{1}{2}$(55°−15°)=20°.故选B.
∵∠ABD,∠ACD的平分线交于点P,
∴∠1=∠2,∠3=∠4.由三角形的内角和定理得,∠A+∠1=∠P+∠3.①在△PBE中,∠5=∠2+∠P,在△DCE中,∠5=∠4−∠D,
∴∠2+∠P=∠4−∠D.②①−②得∠A−∠P=∠P+∠D,
∴∠P=$\frac{1}{2}$(∠A−∠D).
∵∠A=55°,∠D=15°,
∴∠P=$\frac{1}{2}$(55°−15°)=20°.故选B.
(1)观察“规形图”,试探究∠D与∠BAC,∠B,∠C之间的数量关系,并说明理由.
解决问题:
(2)请你利用以上结论,解决下列问题:
①如图(2),把一块含45°角的三角尺DEF放置在△ABC上,使三角尺的两条直角边DE,DF恰好经过点B,C,若∠A= 40°,则∠ABD+∠ACD=
②如图(3),BD平分∠ABP,CD平分∠ACP,若∠A= 40°,∠P= 130°,则∠D的度数为
解决问题:
(2)请你利用以上结论,解决下列问题:
①如图(2),把一块含45°角的三角尺DEF放置在△ABC上,使三角尺的两条直角边DE,DF恰好经过点B,C,若∠A= 40°,则∠ABD+∠ACD=
50
°.②如图(3),BD平分∠ABP,CD平分∠ACP,若∠A= 40°,∠P= 130°,则∠D的度数为
85
.
答案:
[解]
(1)∠BDC=∠BAC+∠B+∠C.理由:如图,连接AD并延长至点F.
根据外角的性质,可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD.又
∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠BAC+∠B+∠C.
(2)①由
(1)可得∠D=∠ABD+∠ACD+∠A,又
∵∠A=40°,∠D=90°,
∴∠ABD+∠ACD=90°−40°=50°,故答案为50.②由
(1)可得∠P=∠A+∠ABP+∠ACP,∠D=∠A+∠ABD+∠ACD,
∴∠ABP+∠ACP=∠P−∠A=130°−40°=90°.又
∵BD平分∠ABP,CD平分∠ACP,
∴∠ABD+∠ACD=$\frac{1}{2}$(∠ABP+∠ACP)=45°,
∴∠D=45°+40°=85°.故答案为85°.
(1)∠BDC=∠BAC+∠B+∠C.理由:如图,连接AD并延长至点F.
根据外角的性质,可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD.又
∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠BAC+∠B+∠C.
(2)①由
(1)可得∠D=∠ABD+∠ACD+∠A,又
∵∠A=40°,∠D=90°,
∴∠ABD+∠ACD=90°−40°=50°,故答案为50.②由
(1)可得∠P=∠A+∠ABP+∠ACP,∠D=∠A+∠ABD+∠ACD,
∴∠ABP+∠ACP=∠P−∠A=130°−40°=90°.又
∵BD平分∠ABP,CD平分∠ACP,
∴∠ABD+∠ACD=$\frac{1}{2}$(∠ABP+∠ACP)=45°,
∴∠D=45°+40°=85°.故答案为85°.
5 [中]如图,∠A= ∠C= 90°,AD,BC交于点E,∠2= 27°,则∠1的大小为 (
A.53°
B.43°
C.37°
D.27°
D
)A.53°
B.43°
C.37°
D.27°
答案:
D [解析]由对顶角相等得∠CED=∠AEB.
∵∠A=∠C=90°,
∴∠CED+∠1=90°,∠AEB+∠2=90°,
∴∠1=∠2=27°.故选D.
∵∠A=∠C=90°,
∴∠CED+∠1=90°,∠AEB+∠2=90°,
∴∠1=∠2=27°.故选D.
6 [2024湖北武汉校级期中,中]如图,∠BAD与∠BCE的平分线交于点P,BC交AD于O,CE的反向延长线交AD于D,则∠P与∠B,∠D的数量关系是 (
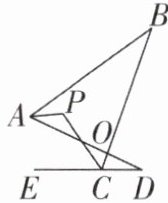
A.2∠P-∠B+∠D= 180°
B.2∠P-∠B-∠D= 180°
C.2∠P+∠B-∠D= 180°
D.2∠P+∠B+∠D= 360°
B
)
A.2∠P-∠B+∠D= 180°
B.2∠P-∠B-∠D= 180°
C.2∠P+∠B-∠D= 180°
D.2∠P+∠B+∠D= 360°
答案:
B [解析]如图,设PC交AD于G,∠PAB=∠OAP=x,∠ECP=∠PCB=y,则∠BAO=2x,∠BCE=2y.
∵∠AOB=∠COD,∠AGP=∠CGD,
∴∠B+∠BAO=∠D+∠OCD,∠P+∠PAG=∠D+∠GCD,
∴$\begin{cases}∠B+2x=∠D+180°-2y,①\\∠P+x=∠D+180°-y,②\end{cases}$①-2×②,可得∠B-2∠P=-∠D-180°,则2∠P-∠B-∠D=180°.故选B.
∵∠AOB=∠COD,∠AGP=∠CGD,
∴∠B+∠BAO=∠D+∠OCD,∠P+∠PAG=∠D+∠GCD,
∴$\begin{cases}∠B+2x=∠D+180°-2y,①\\∠P+x=∠D+180°-y,②\end{cases}$①-2×②,可得∠B-2∠P=-∠D-180°,则2∠P-∠B-∠D=180°.故选B.
查看更多完整答案,请扫码查看


