《2025年初中必刷题八年级数学上册沪科版》

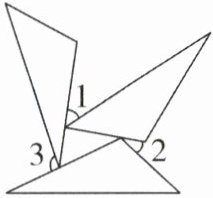
1 [2025 山东烟台期末,中]三个全等三角形按如图所示方式摆放,则∠1 + ∠2 + ∠3 = ( )


A.160°
B.180°
C.200°
D.240°

答案：
1.B　[解析]由全等三角形的性质得到∠4=∠D,∠5=∠6.
∵∠6+∠D+∠BCD=180°,
∴∠4+∠5+∠BCD=180°.
∵∠1+∠4+∠3+∠5+∠2+∠BCD=360°,
∴∠1+∠2+∠3=180°.故选B.

2 [较难]如图所示,锐角三角形 ABC 中,D,E 分别是 AB,AC 边上的点,△ADC≌△ADC',△AEB≌△AEB',且 C'D//EB'//BC,BE,CD 交于点 F,若∠BAC = 40°,则∠BFC 的度数是 ( )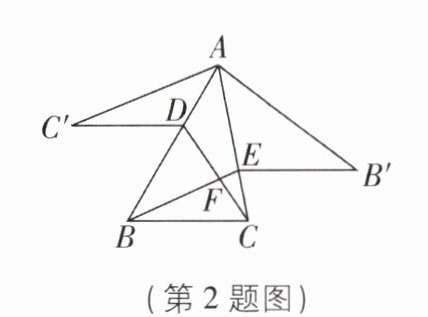

A.105°
B.100°
C.110°
D.115°

答案：
2.B　[解析]如图，延长C'D交AB'于H.

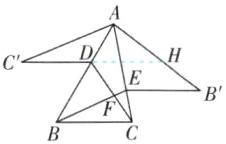
∵△AEB≌△AEB',
∴∠ABE=∠AB'E,∠BAE=∠B'AE.
∵C'H//EB',
∴∠AHC'=∠AB'E,
∴∠ABE=∠AHC'.
∵△ADC≌△ADC',
∴∠C'=∠ACD,∠CAD=∠C'AD.
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC'+∠C'+∠DAC.
∵∠DAC=∠DAC'=∠CAB'=40°,
∴∠C'AH=120°,
∴∠C'+∠AHC'=60°,
∴∠BFC=60°+40°=100°,故选B.

3 [中]如图,在平面直角坐标系中,△OAB 的顶点坐标分别是 O(0,0),A(-6,0),B(0,4),△OA'B'≌△AOB,若点 A'在 x 轴上,则点 B'的坐标是(6,−4).

答案： 3.(6,−4)　[解析]
∵A(−6,0),B(0,4),△OA'B'≌△AOB,
∴OA=OA'=6,OB=A'B'=4,∠OA'B'=∠AOB=90°,
∴点B'的坐标是(6,−4),故答案为(6,−4).

4 [2025 湖南岳阳岳阳楼区校级期中,较难]在四边形 ABCD 中,O 是边 BC 上的一点,如果△OAB 与△OCD 全等,那么点 O 叫作该四边形的“等形点”. 在四边形 EFGH 中,∠EFG = 90°,EF//GH,EF = 1,FG = 3,如果该四边形的“等形点”O 在边 GF 上,那么 GH 的长是____.

答案：
4.1或2　[解析]
∵∠EFG=90°,EF//GH,
∴∠FGH=90°.
∵四边形EFGH的“等形点”O在边FG上,
∴有以下两种情况:如图
(1)，当△OEF≌△OHG时,EF=HG=1.如图
(2)，当△OEF≌△HOG时,EF=OG=1,OF=GH;
∵FG=3,
∴OF=FG−OG=3−1=2,
∴GH=2.
易错警示注意分两种情况讨论:△OEF≌△OHG和△OEF≌△HOG.

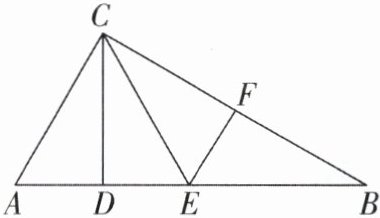
5 [中]如图所示,已知△ABC,其中△ACD≌△ECD,△CEF≌△BEF,∠ACB = 90°.
(1)求证:CD⊥AB;
(2)求∠B 的度数;
(3)求证:EF//AC.

答案： 5.
(1)[证明]
∵△ACD≌△ECD,
∴∠ADC=∠EDC.
∵点A,D,E,B共线,
∴∠ADC+∠EDC=180°,
∴∠ADC=∠EDC=90°,
∴CD⊥AB.
易错警示当用文字语言表示全等时，不能体现各边的对应关系，需要分情况讨论.
(2)[解]设∠B=α.
∵△ACD≌△ECD,△CEF≌△BEF,
∴∠A=∠CED,∠B=∠BCE=α.
∵∠CED=∠B+∠BCE=2α=∠A,∠A+∠B+∠ACB=180°,∠ACB=90°,
∴2α+α+90°=180°,
∴α=30°,即∠B=30°.
(3)[证明]
∵△CEF≌△BEF,
∴∠EFC=∠EFB.又
∵∠EFB+∠EFC=180°,
∴∠EFB=90°.
∵∠ACB=90°,
∴∠ACB=∠EFB,
∴EF//AC.

6 思想方法分类讨论 [难]如图(1),在 Rt△ABC 中,∠C = 90°,BC = 9 cm,AC = 12 cm,AB = 15 cm,现有一动点 P,从点 A 出发,沿着三角形的边 AC→CB→BA 运动,回到点 A 停止,速度为3 cm/s,设运动时间为 t s.
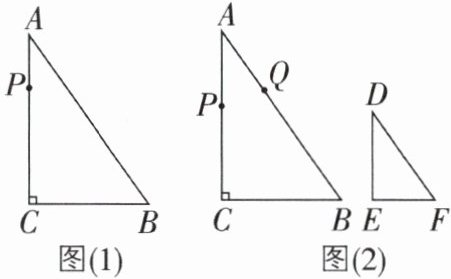
(1)如图(1),当 t = ____时,△APC 的面积等于△ABC 面积的一半;
(2)如图(2),在△DEF 中,∠E = 90°,DE = 4 cm,DF = 5 cm,∠D = ∠A. 在△ABC 的边上,若另外有一个动点 Q,从点 A 出发,沿着边 AB→BC→CA 运动,回到点 A 停止. P,Q 两点同时出发,在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点 Q 的运动速度.

答案：
6.[解]
(1)分两种情况:①当点P在BC上时，若△APC的面积等于△ABC面积的一半,则CP=$\frac{1}{2}$BC=$\frac{9}{2}$cm,此时点P运动的路程为AC+CP=12+$\frac{9}{2}$=$\frac{33}{2}$(cm)，运动的时间为$\frac{33}{2}$÷3=$\frac{11}{2}$(s);②当点P在BA上时，若△APC的面积等于△ABC面积的一半,则BP=$\frac{1}{2}$AB=$\frac{15}{2}$cm,此时点P运动的路程为AC+CB+BP=12+9+$\frac{15}{2}$=$\frac{57}{2}$(cm)，运动的时间为$\frac{57}{2}$÷3=$\frac{19}{2}$(s).故答案为$\frac{11}{2}$或$\frac{19}{2}$.
(2)分两种情况:
①当点P在AC上时，如图
(1)所示,此时AP=4cm,AQ=5cm,
∴点Q运动的速度为5÷(4÷3)=$\frac{15}{4}$(cm/s);
思路分析根据全等三角形的性质和点的坐标得出OA=OA'=6,OB=A'B'=4,∠OA'B'=∠AOB=90°,即可得出答案.

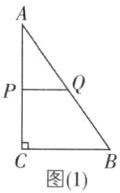
②当点P在AB上时,如图
(2)所示,此时AP=4cm,AQ=5cm,点P运动的路程为9+12+15−4=32(cm),点Q运动的路程为9+12+15−5=31(cm),
∴点Q运动的速度为31÷(32÷3)=$\frac{93}{32}$(cm/s).综上所述，点Q的运动速度为$\frac{15}{4}$cm/s或$\frac{93}{32}$cm/s.