第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2025 安徽合肥期末,中]如图,在$\triangle ABC和\triangle BDE$中,$AC = BC = BE = DE$,$\angle C与\angle E$互补,$BD = 2AB = 8$,则$\triangle ABC$的面积为( )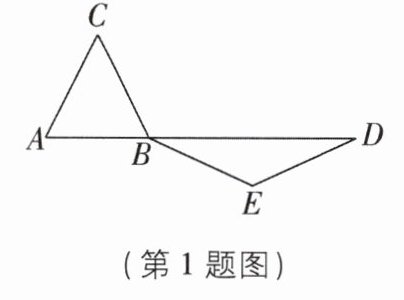
A.$8$
B.$9$
C.$10$
D.$12$

A.$8$
B.$9$
C.$10$
D.$12$
答案:
A [解析]如图,
过点C作CG⊥AB于点G,过点E作EH⊥BD于点H,
则∠CGB = ∠BHE = 90°,
∴∠BCG + ∠CBG = °0°。
∵BD = 2AB = 8,
∴AB = 4。
∵AC = BC = BE = DE,CG⊥AB,EH⊥BD,∠ACB与∠BED互补,
∴∠BCG = $\frac{1}{2}∠ACB$,∠BEH = $\frac{1}{2}∠BED$,BH = $\frac{1}{2}BD = 4$,
∠ACB + ∠BED = l80°,
∴∠BCG + ∠BEH = $\frac{1}{2}×180^{\circ}= 90^{\circ}$,
∴∠CBG = ∠BEH。
在△CBG和△BEH中,$\begin{cases} ∠CGB = ∠BHE\\ ∠CBG = ∠BEH\\ BC = EB \end{cases}$
∴△CBG≌△BEH(AAs),
∴CG = BH = 4,
∴△ABC的面积为$\frac{1}{2}AB\cdot CG = \frac{1}{2}×4×4 = 8$,故选A。

A [解析]如图,
过点C作CG⊥AB于点G,过点E作EH⊥BD于点H,
则∠CGB = ∠BHE = 90°,
∴∠BCG + ∠CBG = °0°。
∵BD = 2AB = 8,
∴AB = 4。
∵AC = BC = BE = DE,CG⊥AB,EH⊥BD,∠ACB与∠BED互补,
∴∠BCG = $\frac{1}{2}∠ACB$,∠BEH = $\frac{1}{2}∠BED$,BH = $\frac{1}{2}BD = 4$,
∠ACB + ∠BED = l80°,
∴∠BCG + ∠BEH = $\frac{1}{2}×180^{\circ}= 90^{\circ}$,
∴∠CBG = ∠BEH。
在△CBG和△BEH中,$\begin{cases} ∠CGB = ∠BHE\\ ∠CBG = ∠BEH\\ BC = EB \end{cases}$
∴△CBG≌△BEH(AAs),
∴CG = BH = 4,
∴△ABC的面积为$\frac{1}{2}AB\cdot CG = \frac{1}{2}×4×4 = 8$,故选A。

2 [2025 安徽亳州期末,较难]如图,已知$\triangle ABC$是等边三角形,点$D是直线AB$上一点,以$CD为边向上作等边三角形CDE$,连接$AE$,则下列结论中错误的是( )
A.当$AD = AE$时,$AC是DE$的垂直平分线
B.当$CD \perp AB$时,$\triangle CDE$的面积最小
C.$AE // BC$
D.$AC = AD + AE$
D
A.当$AD = AE$时,$AC是DE$的垂直平分线
B.当$CD \perp AB$时,$\triangle CDE$的面积最小
C.$AE // BC$
D.$AC = AD + AE$
答案:
D [解析]
∵△ABC和△CDE是等边三角形,
∴CD = CE,BC = AC。
当AD = AE时,AC是DE的垂直平分线,故A选项不符合题意。
当CD最小时,△CDE的面积最小,
∴当CD⊥AB时,△CDE的面积最小,故B选项不符合题意。
∵∠BCA = ∠DCE = 60°,
∴∠BCA - ∠ACD = ∠DCE - ∠ACD,即∠BCD = ∠ACE。
在△BDC与△AEC中,$\begin{cases} BC = AC\\ ∠BCD = ∠ACE\\ DC = EC \end{cases}$
∴△BDC≌△AEC(SAS),
∴∠B = ∠CAE,
∴∠B = ∠CAE = ∠BAC = 60°,
∴∠CAE + ∠BAC = ∠BAE = 120°,
∴∠B + ∠BAE = 180°,
∴AE//BC,故C选项不符合题意。
当点D在线段AB上时,
∵△BDC≌△AEC,
∴AE = BD,
∴AB = AC = AD + AE。
当点D在线段AB的延长线上时,易得AD = AC + AE,故D选项符合题意,故选D。
关键点拨:
(2)若OM边上不存在点$B_{3}$,使得$A_{3}B_{3}=B_{2}A_{3}$,则$∠A_{3}B_{2}M$的度数最小为90°。
思路分析:由题意可得CD = CE,若AD = AE,则AC是DE的垂直平分线,故A选项不符合题意;由等边三角形的面积公式可得当CD⊥AB时,△CDE的面积最小,故B选项不符合题意;证明△BDC≌△AEC,可得∠B = ∠CAE = 60°,进而可证AE//BC,故C选项不符合题意;当点D在线段AB的延长线上时,AD = AC + AE,故D选项符合题意。
∵△ABC和△CDE是等边三角形,
∴CD = CE,BC = AC。
当AD = AE时,AC是DE的垂直平分线,故A选项不符合题意。
当CD最小时,△CDE的面积最小,
∴当CD⊥AB时,△CDE的面积最小,故B选项不符合题意。
∵∠BCA = ∠DCE = 60°,
∴∠BCA - ∠ACD = ∠DCE - ∠ACD,即∠BCD = ∠ACE。
在△BDC与△AEC中,$\begin{cases} BC = AC\\ ∠BCD = ∠ACE\\ DC = EC \end{cases}$
∴△BDC≌△AEC(SAS),
∴∠B = ∠CAE,
∴∠B = ∠CAE = ∠BAC = 60°,
∴∠CAE + ∠BAC = ∠BAE = 120°,
∴∠B + ∠BAE = 180°,
∴AE//BC,故C选项不符合题意。
当点D在线段AB上时,
∵△BDC≌△AEC,
∴AE = BD,
∴AB = AC = AD + AE。
当点D在线段AB的延长线上时,易得AD = AC + AE,故D选项符合题意,故选D。
关键点拨:
(2)若OM边上不存在点$B_{3}$,使得$A_{3}B_{3}=B_{2}A_{3}$,则$∠A_{3}B_{2}M$的度数最小为90°。
思路分析:由题意可得CD = CE,若AD = AE,则AC是DE的垂直平分线,故A选项不符合题意;由等边三角形的面积公式可得当CD⊥AB时,△CDE的面积最小,故B选项不符合题意;证明△BDC≌△AEC,可得∠B = ∠CAE = 60°,进而可证AE//BC,故C选项不符合题意;当点D在线段AB的延长线上时,AD = AC + AE,故D选项符合题意。
(1)当$\angle MB_1A_2 = 45^{\circ}$时,$\angle MON = $
(2)若$OM边上不存在点B_3$,使得$A_3B_3 = B_2A_3$,则$\angle MON$的度数最小是
15°
;(2)若$OM边上不存在点B_3$,使得$A_3B_3 = B_2A_3$,则$\angle MON$的度数最小是
18°
。
答案:
(1)15°
(2)18° [解析]
(1)
∵$OA_{1}=A_{1}B_{1}=B_{1}A_{2}$,
∴∠MON = ∠$A_{1}B_{1}O$,∠$B_{1}A_{1}A_{2}$=∠$B_{1}A_{2}A_{1}$。
∵∠$B_{1}A_{1}A_{2}$=∠MON + ∠$A_{1}B_{1}O$,∠$MB_{1}A_{2}$=∠MON + ∠$B_{1}A_{2}A_{1}$,
∴∠$B_{1}A_{1}A_{2}$=2∠MON,∠$MB_{1}A_{2}$=3∠MON = 45°,
∴∠MON = 15°,故答案为15°。
(2)
∵$B_{1}A_{2}=A_{2}B_{2}=B_{2}A_{3}$,
∴∠$A_{2}B_{1}M$=∠$A_{2}B_{2}B_{1}$=3∠MON,∠$B_{2}A_{2}A_{3}$=∠$B_{2}A_{3}A_{2}$。
∵∠$B_{2}A_{2}A_{3}$=∠MON + ∠$A_{2}B_{2}B_{1}$=4∠MON,
∴∠$MB_{2}A_{3}$=∠MON + ∠$B_{2}A_{3}A_{2}$=5∠MON。
∵OM边上不存在点$B_{3}$,使得$A_{3}B_{3}=B_{2}A_{3}$,
∴∠$MB_{2}A_{3}$的度数最小是90°,
∴5∠MON = 90°,
∴∠MON的度数最小是18°。故答案为18°。
(1)15°
(2)18° [解析]
(1)
∵$OA_{1}=A_{1}B_{1}=B_{1}A_{2}$,
∴∠MON = ∠$A_{1}B_{1}O$,∠$B_{1}A_{1}A_{2}$=∠$B_{1}A_{2}A_{1}$。
∵∠$B_{1}A_{1}A_{2}$=∠MON + ∠$A_{1}B_{1}O$,∠$MB_{1}A_{2}$=∠MON + ∠$B_{1}A_{2}A_{1}$,
∴∠$B_{1}A_{1}A_{2}$=2∠MON,∠$MB_{1}A_{2}$=3∠MON = 45°,
∴∠MON = 15°,故答案为15°。
(2)
∵$B_{1}A_{2}=A_{2}B_{2}=B_{2}A_{3}$,
∴∠$A_{2}B_{1}M$=∠$A_{2}B_{2}B_{1}$=3∠MON,∠$B_{2}A_{2}A_{3}$=∠$B_{2}A_{3}A_{2}$。
∵∠$B_{2}A_{2}A_{3}$=∠MON + ∠$A_{2}B_{2}B_{1}$=4∠MON,
∴∠$MB_{2}A_{3}$=∠MON + ∠$B_{2}A_{3}A_{2}$=5∠MON。
∵OM边上不存在点$B_{3}$,使得$A_{3}B_{3}=B_{2}A_{3}$,
∴∠$MB_{2}A_{3}$的度数最小是90°,
∴5∠MON = 90°,
∴∠MON的度数最小是18°。故答案为18°。
4 [较难]如图,在$\triangle ABC$中,$AB = AC$,点$D在BC$上,且$BD = BA$,点$E在BC$的延长线上,且$CE = CA$。
(1)如图(1),若$\angle BAC = 90^{\circ}$,求$\angle DAE$的度数;
(2)如图(2),若$\angle BAC = 120^{\circ}$,求$\angle DAE$的度数;
(3)当$\angle BAC > 90^{\circ}$时,写出$\angle DAE与\angle BAC$之间的数量关系,并说明理由。
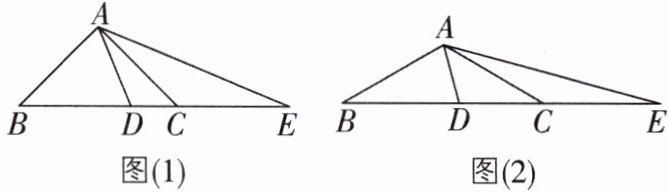
(1)如图(1),若$\angle BAC = 90^{\circ}$,求$\angle DAE$的度数;
(2)如图(2),若$\angle BAC = 120^{\circ}$,求$\angle DAE$的度数;
(3)当$\angle BAC > 90^{\circ}$时,写出$\angle DAE与\angle BAC$之间的数量关系,并说明理由。

答案:
【解】
(1)
∵AB = AC,∠BAC = 90°,
∴∠B = ∠ACB = 45°。
∵BD = BA,
∴∠BAD = ∠BDA = $\frac{1}{2}(180^{\circ}-∠B)= 67.5^{\circ}$。
∵CE = CA,
∴∠CAE = ∠E = $\frac{1}{2}∠ACB = 22.5^{\circ}$,
∴∠BAE = 180° - ∠B - ∠E = 112.5°,
∴∠DAE = ∠BAE - ∠BAD = 45°。
(2)
∵AB = AC,∠BAC = 120°,
∴∠B = ∠ACB = 30°。
∵BA = BD,
∴∠BAD = ∠BDA = 75°,
∴∠DAC = 45°。
∵CA = CE,
∴∠E = ∠CAE = 15°,
∴∠DAE = ∠DAC + ∠CAE = 60°。
(3)∠DAE = $\frac{1}{2}∠BAC$。
理由:设∠CAE = x,∠BAD = y,则∠B = 180° - 2y,∠E = ∠CAE = x,
∴∠BAE = 180° - ∠B - ∠E = 2y - x,
∴∠DAE = ∠BAE - ∠BAD = 2y - x - y = y - x,
∠BAC = ∠BAE - ∠CAE = 2y - x - x = 2y - 2x,
∴∠DAE = $\frac{1}{2}∠BAC$。
(1)
∵AB = AC,∠BAC = 90°,
∴∠B = ∠ACB = 45°。
∵BD = BA,
∴∠BAD = ∠BDA = $\frac{1}{2}(180^{\circ}-∠B)= 67.5^{\circ}$。
∵CE = CA,
∴∠CAE = ∠E = $\frac{1}{2}∠ACB = 22.5^{\circ}$,
∴∠BAE = 180° - ∠B - ∠E = 112.5°,
∴∠DAE = ∠BAE - ∠BAD = 45°。
(2)
∵AB = AC,∠BAC = 120°,
∴∠B = ∠ACB = 30°。
∵BA = BD,
∴∠BAD = ∠BDA = 75°,
∴∠DAC = 45°。
∵CA = CE,
∴∠E = ∠CAE = 15°,
∴∠DAE = ∠DAC + ∠CAE = 60°。
(3)∠DAE = $\frac{1}{2}∠BAC$。
理由:设∠CAE = x,∠BAD = y,则∠B = 180° - 2y,∠E = ∠CAE = x,
∴∠BAE = 180° - ∠B - ∠E = 2y - x,
∴∠DAE = ∠BAE - ∠BAD = 2y - x - y = y - x,
∠BAC = ∠BAE - ∠CAE = 2y - x - x = 2y - 2x,
∴∠DAE = $\frac{1}{2}∠BAC$。
5 核心素养 推理能力 [2025 安徽亳州期末,难]如图(1),在等边$\triangle ABC$中,点$P$,$Q分别是边AB$,$BC$上的动点(端点除外),点$P$,$Q分别从顶点A$,$B$同时出发,以相同的速度向点$B$,$C$匀速运动,连接$AQ$,$CP交于点M$。
(1)求证:$AQ = CP$。
(2)在点$P$,$Q$运动过程中,$\angle QMC$的大小变化吗?若变化,请说明理由;若不变,请直接写出它的度数。
(3)如图(2),若点$P$,$Q在运动到终点后继续在射线AB$,$BC$上运动,直线$AQ$,$CP交点为M$,$\angle QMC$的大小变化吗?若变化,请说明理由;若不变,求出它的度数。
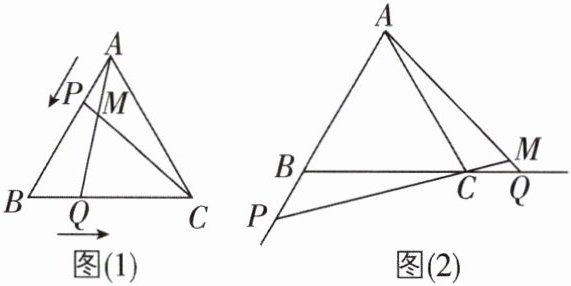
(1)求证:$AQ = CP$。
(2)在点$P$,$Q$运动过程中,$\angle QMC$的大小变化吗?若变化,请说明理由;若不变,请直接写出它的度数。
(3)如图(2),若点$P$,$Q在运动到终点后继续在射线AB$,$BC$上运动,直线$AQ$,$CP交点为M$,$\angle QMC$的大小变化吗?若变化,请说明理由;若不变,求出它的度数。

答案:
(1)【证明】
∵△ABC为等边三角形,
∴AB = AC,∠BAC = ∠ABC = 60°。
∵点P,Q分别从顶点A,B同时出发,以相同的速度向点B,C匀速运动,
∴AP = BQ。
在△ABQ和△CAP中,$\begin{cases} AB = CA\\ ∠ABQ = ∠CAP\\ BQ = AP \end{cases}$
∴△ABQ≌△CAP(SAS),
∴AQ = CP。
(2)【解】∠QMC的大小不变,为60°。
由
(1)可知△ABQ≌△CAP,
∴∠BAQ = ∠ACP。
∵∠QMC是△ACM的外角,
∴∠QMC = ∠MAC + ∠ACM = ∠MAC + ∠BAQ = ∠BAC = 60°。
(3)【解】∠QMC的大小不变。
由题意得BP = CQ,
∴AP = BQ。
在△ABQ和△CAP中,$\begin{cases} AB = AC\\ ∠ABQ = ∠CAP\\ BQ = AP \end{cases}$
∴△ABQ≌△CAP(SAS),
∴∠BAQ = ∠ACP。
∵∠QMC是△APM的外角,
∴∠QMC = ∠PAM + ∠APC = ∠ACP + ∠APC = 180° - 60° = 120°。
(1)【证明】
∵△ABC为等边三角形,
∴AB = AC,∠BAC = ∠ABC = 60°。
∵点P,Q分别从顶点A,B同时出发,以相同的速度向点B,C匀速运动,
∴AP = BQ。
在△ABQ和△CAP中,$\begin{cases} AB = CA\\ ∠ABQ = ∠CAP\\ BQ = AP \end{cases}$
∴△ABQ≌△CAP(SAS),
∴AQ = CP。
(2)【解】∠QMC的大小不变,为60°。
由
(1)可知△ABQ≌△CAP,
∴∠BAQ = ∠ACP。
∵∠QMC是△ACM的外角,
∴∠QMC = ∠MAC + ∠ACM = ∠MAC + ∠BAQ = ∠BAC = 60°。
(3)【解】∠QMC的大小不变。
由题意得BP = CQ,
∴AP = BQ。
在△ABQ和△CAP中,$\begin{cases} AB = AC\\ ∠ABQ = ∠CAP\\ BQ = AP \end{cases}$
∴△ABQ≌△CAP(SAS),
∴∠BAQ = ∠ACP。
∵∠QMC是△APM的外角,
∴∠QMC = ∠PAM + ∠APC = ∠ACP + ∠APC = 180° - 60° = 120°。
查看更多完整答案,请扫码查看


