《2025年初中必刷题八年级数学上册沪科版》

能说明“锐角α,锐角β的和小于90°”是假命题的例证图是(D)
A.
B.
C.
D.

答案： D

甲、乙、丙、丁四个人参加一个比赛,有两个人获奖.在比赛结果揭晓之前,四个人进行了如下猜测:
甲:两名获奖者在乙、丙、丁中.
乙:我没有获奖,丙获奖了.
丙:甲、乙两个人中有且只有一个人获奖.
丁:乙说的对.
已知四个人中有且只有两个人的猜测是正确的,则两名获奖者为(C)
A.甲、丁
B.乙、丙
C.乙、丁
D.以上都不正确

答案： C

其中,真命题有①②④.(填序号)

答案： ①②④

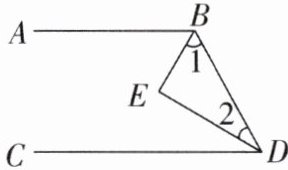
4[2025安徽亳州期末,中]如图,①AB//CD,②BE平分∠ABD,③∠1+∠2= 90°,④DE平分∠BDC.
(1)请以其中三个为条件,另外一个为结论,写出一个命题;
(2)判断这个命题是否为真命题,并说明理由.

答案：
(1)如果BE平分∠ABD,∠1+∠2=90°,DE平分∠BDC,那么AB//CD(答案不唯一).　
(2)这个命题是真命题，理由如下:
∵BE平分∠ABD,
∴∠1=$\frac{1}{2}$∠ABD.
∵DE平分∠BDC,
∴∠2=$\frac{1}{2}$∠BDC.
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB//CD.　(答案不唯一)

(1)判断EM与FN之间的位置关系,并证明你的结论;
EM//FN.证明:
∵∠1+∠2=180°,∠EFD+∠2=180°,
∴∠1=∠EFD,
∴AB//CD,
∴∠BEF=∠CFE.
∵EM,FN分别平分∠BEF和∠CFE,
∴∠NFE=∠MEF,
∴EM//FN
(2)由(1)的结论我们可以得到一个命题:
如果两条平行线被第三条直线所截,那么一组内错角的平分线互相平行;
(3)由此可以探究并得到:
如果两条平行线被第三条直线所截,那么一组同旁内角的平分线互相垂直.

答案：
(1)EM//FN.证明:
∵∠1+∠2=180°,∠EFD+∠2=180°,
∴∠1=∠EFD,
∴AB//CD,
∴∠BEF=∠CFE.
∵EM,FN分别平分∠BEF和∠CFE,
∴∠NFE=∠MEF,
∴EM//FN;　
(2)平行　
(3)垂直