《2025年初中必刷题八年级数学上册沪科版》

一、选择题(共 40 分)
1 [2025 广东湛江质检]下列各组图案中,属于全等形的是 (A)

答案： A 【解析】观察各选项,只有选项A中的两个图案能够完全重合,选项B、C、D中的两个图案不能够完全重合. 故选A.

2 根据下列已知条件,不能画出唯一△ABC 的是 (C)
A.AB = 3,BC = 6,CA = 8

B.AB = 6,∠B = 60°,BC = 10
C.AB = 4,BC = 3,∠A = 30°
D.∠A = 60°,∠B = 45°,AB = 4

答案： C 【解析】AB = 3,BC = 6,CA = 8,符合全等三角形的判定定理SSS,能画出唯一的△ABC,故不符合题意；AB = 6,∠B = 60°,BC = 10,符合全等三角形的判定定理SAS,能画出唯一的△ABC,故不符合题意；AB = 4,BC = 3,∠A = 30°,不符合全等三角形的判定定理,不能画出唯一的△ABC,故符合题意；∠A = 60°,AB = 4,∠B = 45°,符合全等三角形的判定定理ASA,能画出唯一的△ABC,故不符合题意.

3 [2025 安徽合肥期中]如图所示,D,E 分别是△ABC 的边 AC,BC 上的点,若△ADB ≌ △EDB ≌ △EDC,则∠C 的度数为 (D)

A.15°
B.20°
C.25°
D.30°

答案： D 【解析】
∵△ADB≌△EDB≌△EDC,
∴∠A = ∠BED = ∠CED,∠ABD = ∠EBD = ∠C.
∵∠BED+∠CED = 180°,
∴∠A = ∠BED = ∠CED = 90°.在△ABC中,∠C+2∠C+90° = 180°,
∴∠C = 30°. 故选D.

要测量池塘两端 A,B 间的距离(无法直接测出),两位同学提供了如下测量方案.
方案Ⅰ:①如图(1),选定点 O;②连接 AO 并延长到点 C,使 OC = OA,连接 BO 并延长到点 D,使 OD = OB;③连接 DC,测量 DC 的长度即可.
方案Ⅱ:①如图(2),选定点 O;②连接 AO,BO,并分别延长到点 F,E,使 OF = OB,OE = OA;③连接 EF,测量 EF 的长度即可.
对于方案Ⅰ、Ⅱ,下列说法正确的是 (D)
A.Ⅰ可行、Ⅱ不可行
B.Ⅰ不可行、Ⅱ可行

C.Ⅰ、Ⅱ都不可行
D.Ⅰ、Ⅱ都可行

答案： D 【解析】方案Ⅰ:在△AOB与△COD中,AO = OC,∠AOB = ∠COD,OB = OD,
∴△AOB≌△COD(SAS),
∴AB = CD,
∴方案Ⅰ可行.方案Ⅱ:在△AOB与△EOF中,AO = EO,∠AOB = ∠EOF,OB = OF,
∴△AOB≌△EOF(SAS),
∴AB = EF,
∴方案Ⅱ可行. 故选D.

5 [2025 山东德州期中]如图,△ABC 中 BC 边上的高为$ h_1,△DEF $中 DE 边上的高为$ h_2,$若 AC = EF,下列结论中正确的是 ( C )

$A. h_1 ＜ h_2 B. h_1 ＞ h_2$
$C. h_1 = h_2 D. $无法确定

答案： C 【解析】过点A作AM⊥BC交BC于点M,过点F作FN⊥DE交DE的延长线于点N,如图所示,则AM = h₁,FN = h₂.
∵AM⊥BC,FN⊥DE,
∴∠AMC = ∠FNE = 90°.
∵∠FEN = ∠FDE+∠DFE = 35°+30° = 65°,
∴∠ACM = ∠FEN.在△AMC和△FNE中,∠AMC = ∠FNE,∠ACM = ∠FEN,AC = EF,
∴△AMC≌△FNE(AAS),
∴AM = FN,即h₁ = h₂,故选C.

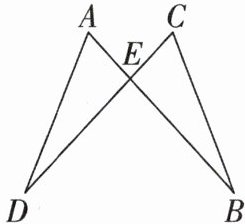
6 如图,AB,CD 相交于点 E,且 AB = CD,试添加一个条件使得△ADE ≌ △CBE. 现给出如下五个条件:①∠A = ∠C;②∠B = ∠D;③AE = CE;④BE = DE;⑤AD = CB. 其中符合要求的有 (A)

A.5 个
B.4 个
C.3 个
D.2 个

答案： A 【解析】延长DA,BC交于点F.
∵∠DAB = ∠BCD,∠AED = ∠BEC,
∴∠ABC = ∠CDA.在△FAB 和△FCD中,∠FBA = ∠FDC,∠F = ∠F,AB = CD,
∴△FAB≌△FCD(AAS),
∴AF = FC,FD = FB,
∴AD = BC.在△ADE和△CBE中,∠AED = ∠CEB,∠ADE = ∠CBE,AD = CB,
∴△ADE≌△CBE(AAS),故①符合题意,同理可得②符合题意.
∵AE = CE,AB = CD,
∴DE = BE.在△ADE和△CBE中,AE = CE,∠AED = ∠BEC,DE = BE,
∴△ADE≌△CBE(SAS),故③符合题意,同理可得④符合题意.连接BD.在△ADB和△CBD中,AD = CB,AB = CD,BD = BD,
∴△ADB≌△CBD(SSS),
∴∠DAE = ∠BCE.在△ADE和△CBE中,∠DAE = ∠BCE,∠AED = ∠CEB,AD = BC,
∴△ADE≌△CBE(AAS),故⑤符合题意. 故选A.

7 如图,在平面直角坐标系中,点 A(2,0),B(0,4),若以 B,O,C 为顶点的三角形与△ABO 全等,则点 C 的坐标不能为 (A)
A.(0,-4)
B.(-2,0)
C.(2,4)
D.(-2,4)

答案： A 【解析】如图所示.
∵A(2,0),B(0,4),
∴OB = 4,OA = 2.
∵△BOC与△AOB全等,
∴①△AOB≌△COB,
∴OA = OC = 2,∠BOC = ∠AOB = 90°,
∴C₁(-2,0).②△AOB≌△CBO,
∴OA = BC = 2,OB = BO = 4,∠OBC = ∠BOA = 90°,
∴C₂(-2,4),C₃(2,4). 综上可知,点C的坐标为(-2,0)或(2,4)或(-2,4). 故选A.

如图,在△ABC 中,AD 是△BAC 的外角平分线,与 BC 的延长线交于点 D,P 是 AD 上异于 A 的任意一点,连接 PB,PC. 设 PB = m,PC = n,AB = c,AC = b,则 m + n 与 b + c 的大小关系是 (A)
A.m + n ＞ b + c
B.m + n ＜ b + c
C.m + n = b + c
D.无法确定

答案： A 【解析】如图,在BA的延长线上取点E,使AE = AC,连接EP.
∵AD是△ABC的外角平分线,
∴∠CAD = ∠EAD.在△ACP和△AEP中,AC = AE,∠CAD = ∠EAD,AP = AP,
∴△ACP≌△AEP(SAS),
∴PE = PC.在△PBE中,PB+PE＞AB+AE.
∵PB = m,PC = n,AB = c,AC = b,
∴m+n＞b+c. 故选A.