《2025年初中必刷题八年级数学上册沪科版》

如图,AD,BE,CF分别是△ABC的中线、高和角平分线,∠ABC= 90°,CF交AD于点G,交BE于点H,AB= BD。给出下列结论：①AB= CD；②FG= GC；③∠ABE= 2∠FCB；④∠BFH= ∠BHF。其中一定正确的是(A)
A.①③④
B.②③④
C.①②③
D.①②④

答案： A 【解析】因为AD是△ABC的中线，所以BD=CD.又因为AB=BD，所以AB=CD，故①正确.因为BE，CF分别是△ABC的高和角平分线，所以∠AEB=∠BEC=90°，∠ACB=2∠ACF=2∠FCB，所以∠ABE+∠BAC=90°.因为∠ABC=90°，所以∠ACB+∠BAC=90°，所以∠ABE=∠ACB=2∠FCB，故③正确.因为∠ABC=90°，∠BEC=90°，所以∠BFH+∠FCB=90°，∠ECF+∠CHE=90°.因为∠BCF=∠ECF，所以∠BFH=∠CHE.又因为∠CHE=∠BHF，所以∠BFH=∠BHF，故④正确.由已知条件无法得到FG=GC.故选A.

如图$,AP_1$为△ABC的中线$,AP_2$为$△AP_1C$的中线$,AP_3$为$△AP_2C$的中线,…,按此规律,APₙ为$△APₙ₋_1C$的中线。若△ABC的面积为S,则△APₙC的面积为(C)
A.$\frac{S}{2^{n - 2}}$
B.$\frac{S}{2^{n - 1}}$
C.$\frac{S}{2^{n}}$
D.$\frac{S}{2^{n + 1}}$

答案： C 【解析】因为AP1为△ABC的中线，所以S△AP1C = $\frac{1}{2}$S△ABC = $\frac{1}{2}$S.因为AP2为△AP1C的中线，所以S△AP2C = $\frac{1}{2}$S△AP1C = $\frac{1}{2^2}$S.因为AP3为△AP2C的中线，所以S△AP3C = $\frac{1}{2}$S△AP2C = $\frac{1}{2^3}$S，…，按此规律，△APnC的面积为 $\frac{S}{2^n}$.故选C.

3 [中]如图,图(1)中有3个以MN为高的三角形,图(2)中有10个以MN为高的三角形,图(3)中有21个以MN为高的三角形,…,以此类推,则图(6)中以MN为高的三角形的个数为(B)
A.55
B.78
C.96
D.105

答案： B 【解析】题图
(1)中以MN为高的三角形的个数是3 = 2×1² + 1，题图
(2)中以MN为高的三角形的个数是10 = 2×2² + 2，题图
(3)中以MN为高的三角形的个数是21 = 2×3² + 3，…，所以所求的图中以MN为高的三角形的个数是2×6² + 6 = 78，故选B.

4 [2025安徽安庆桐城校级期中,中]如图,CD是△ABC的一条中线,E为BC边上一点,且BE= 2CE,连接AE交CD于F。若四边形BDFE的面积为6,则$S_{△ABE}:S_{△ABC}= $______,$S_{△ABC}= $______。

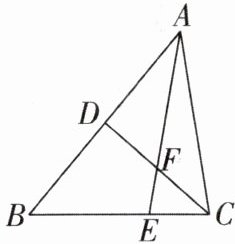
答案：
2:3;14.4 【解析】连接BF，如图所示.设S△BDF = a，则S△BEF = 6 - a.因为CD为AB边上的中线，所以S△ADF = S△BDF = a，S△BDC = $\frac{1}{2}$S△ABC.因为BE = 2CE，所以S△CEF = $\frac{1}{2}$S△BEF = $\frac{1}{2}$(6 - a)，S△ABE = $\frac{2}{3}$S△ABC，即S△ABE:S△ABC = 2:3，所以S△ABC = $\frac{3}{2}$S△ABE = $\frac{3}{2}$(2a + 6 - a) = $\frac{3}{2}$a + 9.因为S△ABC = 2S△BDC = 2[a + (6 - a) + $\frac{1}{2}$(6 - a)] = 18 - a，所以18 - a = $\frac{3}{2}$a + 9，解得a = 3.6，所以S△ABC = 18 - a = 18 - 3.6 = 14.4，故答案为2:3，14.4.

5 [2025安徽安庆质检,较难]在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,将这三条边上的高依次记为$h_a$,$h_b$,$h_c$。
(1)当a= 6,$h_a$= 2,$h_b$= 4时,b= ______。
(2)当$h_a$= 2,$h_b$= 4时,$h_c$的取值范围是______。

答案：

(1)3
(2)$\frac{4}{3}$ ＜ hc ＜ 4 【解析】
(1)因为S△ABC = $\frac{1}{2}$ahₐ = $\frac{1}{2}$bhᵦ，所以b = $\frac{ahₐ}{hᵦ}$ = $\frac{2×6}{4}$ = 3.故答案为3.
(2)

6 [中]如图,在三角形ABC中(AB＞BC),AC= 2BC,BC边上的中线AD把三角形ABC的周长分成70和50两部分,求AC和AB的长。

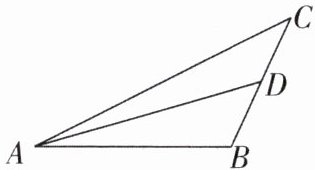
答案： 【解】设BD = CD = x，则AC = 2BC = 4x.①当AC + CD = 70，AB + BD = 50时，4x + x = 70，解得x = 14，所以AC = 4x = 4×14 = 56，BD = CD = 14，BC = 2×14 = 28，所以AB = 50 - BD = 50 - 14 = 36.因为AB = 36 ＞ BC = 28，满足条件，BC + AB = 28 + 36 = 64 ＞ AC = 56，满足三边关系，所以AC = 56，AB = 36.②当AC + CD = 50，AB + BD = 70时，4x + x = 50，解得x = 10，所以AC = 4x = 4×10 = 40，BD = CD = 10，BC = 2×10 = 20，所以AB = 70 - BD = 70 - 10 = 60.因为BC + AC = AB = 60，不满足三边关系，所以舍去.综上，AC = 56，AB = 36.

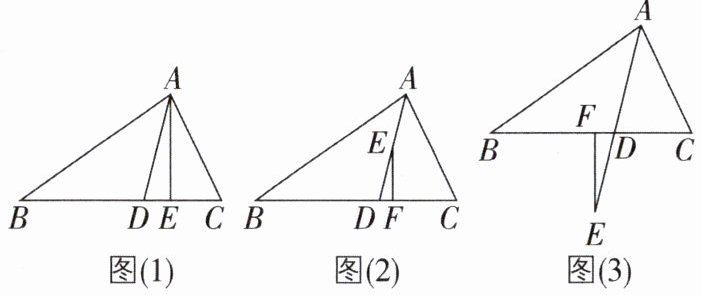
7 核心素养 模型观念 [难]在三角形ABC中,AD是角平分线,∠B＜∠C。
(1)如图(1),AE是高,∠B= 35°,∠C= 65°,求∠DAE的度数；
(2)如图(2),点E在AD上,EF⊥BC于F,试探究∠DEF与∠B,∠C的大小关系,并说明理由；
(3)如图(3),点E在AD的延长线上,EF⊥BC于F,则∠DEF与∠B,∠C的大小关系是______(直接写出结论,不需说明理由)。

答案：
【解】
(1)因为AD平分∠BAC，所以∠CAD = $\frac{1}{2}$∠BAC.因为AE⊥BC，所以∠CAE = 180° - 90° - ∠C，所以∠DAE = ∠CAD - ∠CAE = $\frac{1}{2}$∠BAC - (90° - ∠C) = $\frac{1}{2}$(180° - ∠B - ∠C) - (90° - ∠C) = $\frac{1}{2}$∠C - $\frac{1}{2}$∠B = $\frac{1}{2}$(∠C - ∠B).因为∠B = 35°，∠C = 65°，所以∠DAE = $\frac{1}{2}$(65° - 35°) = 15°.
(2)∠DEF = $\frac{1}{2}$(∠C - ∠B).理由：如图
(1)，过A作AG⊥BC于G.因为EF⊥BC，所以AG//EF，所以∠DAG = ∠DEF.由
(1)可得，∠DAG = $\frac{1}{2}$(∠C - ∠B)，所以∠DEF = $\frac{1}{2}$(∠C - ∠B).

(3)如图
(2)，过A作AG⊥BC于G.因为EF⊥BC于F，所以AG//EF，所以∠DAG = ∠DEF.由
(1)可得，∠DAG = $\frac{1}{2}$(∠C - ∠B)，所以∠DEF = $\frac{1}{2}$(∠C - ∠B)，故答案为∠DEF = $\frac{1}{2}$(∠C - ∠B).

技巧点拨：注意一个三角形中最多有一个直角或最多有一个钝角.
关键点拨：根据三角形的面积公式与中线的性质可得△AP1C的面积是△ABC的面积的一半。利用等底同高三角形面积相等、同高不同底面积的比为底之比，而使用方程来表示面积，进而思考解决问题。注意三角形的形状对结果的影响，本题中根据∠B = 30°不能判断出三角形ABC的形状，需要分类讨论。