第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2025 安徽阜阳质检]下列各组给出的两个图形中,是全等形的是 (
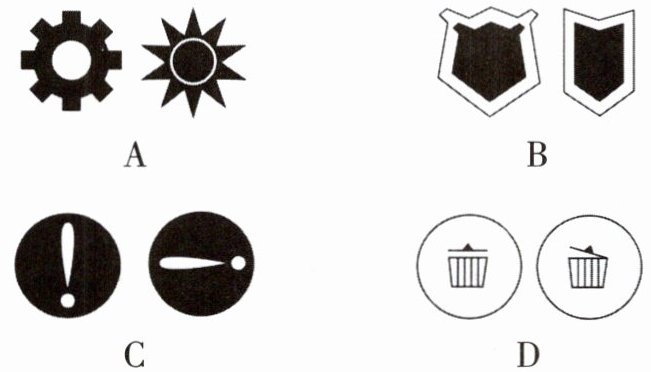
C
)
答案:
1.C [解析]选项A、B、D中的两个图形的形状不一样,不是全等形,故不符合题意;选项C中的两个图形能够完全重合,是全等形,故符合题意,故选C.
如图,已知△ABC 与△BDE 全等,其中点 D 在边AB 上,AC//DE,∠E 的对应角是
∠ABC
.
答案:
2.∠ABC [解析]
∵AC//DE,
∴∠A=∠BDE.
∵△ABC与△BDE全等,∠A=∠BDE,
∴BC与BE是对应边.
∵BD<AB,
∴BD与AC是对应边,
∴△ABC≌△DEB,
∴∠E=∠ABC.故答案为∠ABC.
∵AC//DE,
∴∠A=∠BDE.
∵△ABC与△BDE全等,∠A=∠BDE,
∴BC与BE是对应边.
∵BD<AB,
∴BD与AC是对应边,
∴△ABC≌△DEB,
∴∠E=∠ABC.故答案为∠ABC.
3 [2024 山西大同质检]△ABC 与△DEF 全等,则根据图中提供的信息,可得出x的值为 (
A.30
B.27
C.35
D.40
A
)A.30
B.27
C.35
D.40
答案:
3.A [解析]
∵△ABC与△DEF全等,
∴根据对应角和对应边相等,可以得到BC=EF=30,即x=30.故选A.
∵△ABC与△DEF全等,
∴根据对应角和对应边相等,可以得到BC=EF=30,即x=30.故选A.
4 [2025 安徽安庆质检]如图,在△ABC 中,AD⊥BC于点 D,点 E 在 AD 上,且△CED≌△ABD. 若 DE +DC = 14,DA - DB = 2,则 DE 的长为____

6
.
答案:
4.6 [解析]
∵△CED≌△ABD,
∴AD=CD,由全等三角形的性质得BD=DE,再结合已知条件即可求解.
∵DE+DC=14,DA−DB=2,
∴DE+DA=14,DA−DE=2,
∴DA=8,DE=6,故答案为6.
∵△CED≌△ABD,
∴AD=CD,由全等三角形的性质得BD=DE,再结合已知条件即可求解.
∵DE+DC=14,DA−DB=2,
∴DE+DA=14,DA−DE=2,
∴DA=8,DE=6,故答案为6.
5 [2024 安徽滁州期中]如图,A,E,C 三点在同一直线上,且△ABC≌△DAE.
(1)线段 DE,CE,BC 有怎样的数量关系? 请说明理由.
(2)请你猜想△ADE 满足什么条件时,DE//BC,并证明.

(1)线段 DE,CE,BC 有怎样的数量关系? 请说明理由.
(2)请你猜想△ADE 满足什么条件时,DE//BC,并证明.

答案:
5.[解]
(1)DE=CE+BC.理由:
∵△ABC≌△DAE,
∴AE=BC,DE=AC.
∵A,E,C三点在同一直线上,
∴AC=AE+CE,
∴DE=CE+BC.
(2)当△ADE满足∠AED=90°时,DE//BC.证明:
∵△ABC≌△DAE,∠AED=90°,
∴∠C=∠AED=90°,∠DEC=180°−∠AED=90°,
∴∠C=∠DEC.
∴DE//BC,故当△ADE满足∠AED=90°时,DE//BC.
(1)DE=CE+BC.理由:
∵△ABC≌△DAE,
∴AE=BC,DE=AC.
∵A,E,C三点在同一直线上,
∴AC=AE+CE,
∴DE=CE+BC.
(2)当△ADE满足∠AED=90°时,DE//BC.证明:
∵△ABC≌△DAE,∠AED=90°,
∴∠C=∠AED=90°,∠DEC=180°−∠AED=90°,
∴∠C=∠DEC.
∴DE//BC,故当△ADE满足∠AED=90°时,DE//BC.
6 如图,点 B,C,D 在同一条直线上,∠B = ∠D = 90°,△ABC≌△CDE,AB = 6,BC = 8,CE = 10.
(1)求△ABC 的周长;
(2)求△ACE 的面积.
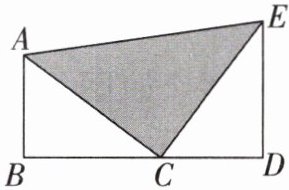

(1)求△ABC 的周长;
(2)求△ACE 的面积.


答案:
6.[解]
(1)
∵△ABC≌△CDE,CE=10,
∴AC=CE=10.
∵AB=6,BC=8,
∴△ABC的周长为AB+BC+AC=6+8+10=24.
(2)
∵∠B=90°,
∴∠ACB+∠BAC=90°.
∵△ABC≌△CDE,
∴∠ECD=∠CAB,
∴∠ACB+∠ECD=90°,
∴∠ACE=90°.
∵AC=CE=10,
∴△ACE的面积为$\frac{1}{2}$×10×10=50.
(1)
∵△ABC≌△CDE,CE=10,
∴AC=CE=10.
∵AB=6,BC=8,
∴△ABC的周长为AB+BC+AC=6+8+10=24.
(2)
∵∠B=90°,
∴∠ACB+∠BAC=90°.
∵△ABC≌△CDE,
∴∠ECD=∠CAB,
∴∠ACB+∠ECD=90°,
∴∠ACE=90°.
∵AC=CE=10,
∴△ACE的面积为$\frac{1}{2}$×10×10=50.
7 边长都为整数的△ABC 和△DEF 全等,AB 与DE 是对应边,AB = 2,BC = 4,若△DEF 的周长为奇数,则 DF 的长为 (
A.3
B.4
C.3 或 5
D.3 或 4 或 5
D
)A.3
B.4
C.3 或 5
D.3 或 4 或 5
答案:
7.D [解析]
∵AB=2,BC=4,
∴2<AC<6.
∵△DEF的周长为奇数,△ABC和△DEF全等,
∴△ABC的周长为奇数,
∴AC的长为奇数,
∴AC的长是3或5.
∵△ABC和△DEF全等,AB与DE是对应边,
∴DE=AB=2.当DF=AC时,DF=3或5.当DF=BC时,DF=4.故选D.
∵AB=2,BC=4,
∴2<AC<6.
∵△DEF的周长为奇数,△ABC和△DEF全等,
∴△ABC的周长为奇数,
∴AC的长为奇数,
∴AC的长是3或5.
∵△ABC和△DEF全等,AB与DE是对应边,
∴DE=AB=2.当DF=AC时,DF=3或5.当DF=BC时,DF=4.故选D.
查看更多完整答案,请扫码查看


