《2025年初中必刷题八年级数学上册沪科版》

(1)探究:如图(1),在△ABC中,∠ACB= 90°,CD⊥AB于点D,若∠B= 30°,则∠ACD的度数是30°;
(2)拓展:如图(2),∠MCN= 90°,射线CP在∠MCN的内部,点A,B分别在CM,CN上,分别过点A,B作AD⊥CP,BE⊥CP,垂足分别为D,E,若∠CBE= 70°,求∠CAD的度数;
∵BE⊥CP,
∴∠BEC=90°.
∵∠CBE=70°,
∴∠BCE=90°−∠CBE=20°.
∵∠MCN=90°,
∴∠ACD=90°−∠BCE=70°.
∵AD⊥CP,
∴∠CAD=90°−∠ACD=20°.
(3)应用:如图(3),点A,B分别在∠MCN的边CM,CN上,射线CP在∠MCN的内部,点D,E在射线CP上,连接AD,BE,若∠ADP= ∠BEP= 60°,则∠CAD+∠CBE+∠ACB=120°.

答案： [解]
(1)在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°.
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=90°−∠A=30°.故答案为30.
(2)
∵BE⊥CP,
∴∠BEC=90°.
∵∠CBE=70°,
∴∠BCE=90°−∠CBE=20°.
∵∠MCN=90°,
∴∠ACD=90°−∠BCE=70°.
∵AD⊥CP,
∴∠CAD=90°−∠ACD=20°.
(3)
∵∠ADP是△ACD的外角,
∴∠ADP=∠ACD+∠CAD=60°,同理,∠BEP=∠BCE+∠CBE=60°,
∴∠CAD+∠CBE+∠ACB=∠CAD+∠CBE+∠ACD+∠BCE=(∠CAD+∠ACD)+(∠CBE+∠BCE)=120°.故答案为120.

13 [2025浙江温州质检,中]如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD= 15°,∠B= 50°,求∠C的度数.

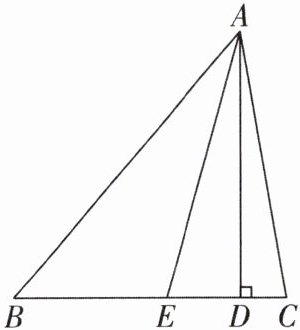
答案： [解]
∵AD是BC边上的高,∠B=50°,
∴∠ADB=90°,
∴∠BAD=90°−50°=40°.
∵∠EAD=15°,
∴∠BAE=∠BAD−∠EAD=40°−15°=25°.
∵AE是∠BAC的平分线,
∴∠BAC=2∠BAE=50°.在△ABC中,∠BAC+∠B+∠C=180°,∠B=50°,∠BAC=50°,
∴∠C=180°−∠B−∠BAC=180°−50°−50°=80°.

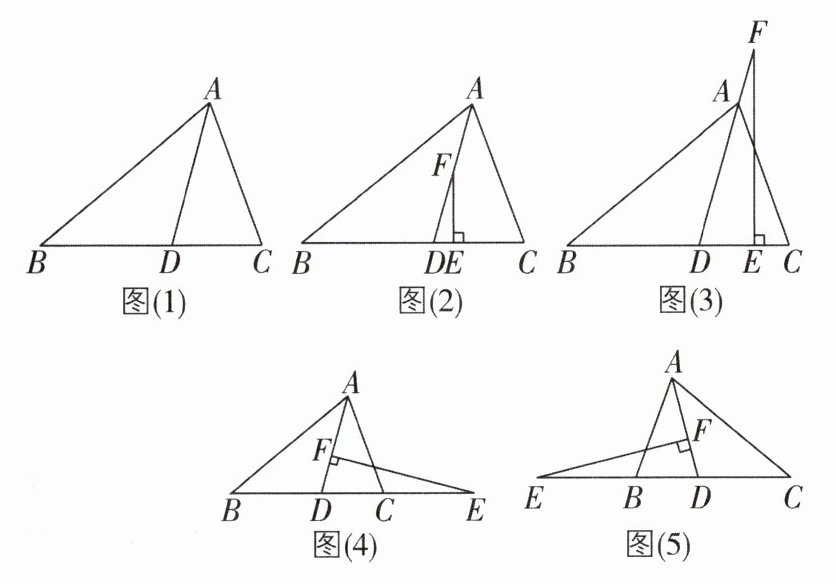
14 [2024河南新乡期中,较难]综合与实践课上,老师让同学们以“三角形的角与三角形的特殊线段”为主题开展数学活动.
【操作判断】(1)在△ABC中,∠B= 40°,∠C= 70°,作∠BAC的平分线AD交BC于点D.
①操作一:在图(1)中,用三角尺作BC边上的高AE,垂足为点E,求∠DAE的度数;
②操作二:如图(2),在AD上任取点F,作FE⊥BC,垂足为点E,直接写出∠DFE的度数.
【迁移探究】(2)如图(3),将操作二中“在AD上任取点F”改为“在DA的延长线上任取点F”,其他条件不变,判断∠DFE的度数是否会发生变化,并说明理由.
【拓展应用】(3)如图(4)、图(5),在△ABC中,∠ABC= α,∠ACB= β,AD是∠BAC的平分线,在直线AD上任取点F,过点F作EF⊥AD与直线BC交于点E,请求出∠DEF与α,β之间的数量关系.

答案： [解]
(1)①如图,AE即为所求.
∵在△ABC中,∠B=40°,∠C=70°,
∴∠BAC=180°−40°−70°=70°.
∵AD是∠BAC的平分线,
∴∠BAD=$\frac{1}{2}$∠BAC=35°.
∵∠ADC是△ABD的一个外角,
∴∠ADC=∠B+∠BAD=40°+35°=75°.
∵用三角尺作BC边上的高AE,垂足为点E,
∴∠DAE=90°−75°=15°.②∠DFE=15°.
∵∠ADC是△ABD的一个外角,
∴∠ADC=∠B+∠BAD=40°+35°=75°.
∵FE⊥BC,
∴∠DFE=90°−∠ADC=15°.
(2)不会发生变化.理由如下:
∵∠BAD=$\frac{1}{2}$∠BAC=35°,∠B=40°,∠ADC是△ABD的一个外角,
∴∠ADC=∠B+∠BAD=40°+35°=75°.
∵FE⊥BC,
∴∠DFE=90°−∠ADC=15°,
∴∠DFE的度数不会发生变化.
(3)如题图
(4)所示,
∵在△ABC中,∠ABC=α,∠ACB=β,
∴∠BAC=180°−α−β.
∵AD是∠BAC的平分线,
∴∠BAD=$\frac{1}{2}$∠BAC=90°−$\frac{\alpha+\beta}{2}$.
∵∠ADC是△ABD的一个外角,
∴∠ADC=∠ABC+∠BAD=α+90°−$\frac{\alpha+\beta}{2}$=90°+$\frac{\alpha-\beta}{2}$.
∵FE⊥AD,
∴∠DEF=90°−∠ADC=90°−(90°+$\frac{\alpha-\beta}{2}$)=$\frac{\beta-\alpha}{2}$.如题图
(5)所示,
∵在△ABC中,∠ABC=α,∠ACB=β,
∴∠BAC=180°−α−β.
∵AD是∠BAC的平分线,
∴∠BAD=$\frac{1}{2}$∠BAC=90°−$\frac{\alpha+\beta}{2}$,
∴∠ADB=180°−∠ABC−∠BAD=180°−α−(90°−$\frac{\alpha+\beta}{2}$)=90°−$\frac{\alpha-\beta}{2}$.
∵FE⊥AD,
∴∠DEF=90°−∠ADB=90°−(90°−$\frac{\alpha-\beta}{2}$)=$\frac{\alpha-\beta}{2}$.综上所述,∠DEF=$\frac{\beta-\alpha}{2}$或∠DEF=$\frac{\alpha-\beta}{2}$.