《2025年初中必刷题八年级数学上册沪科版》

1 [2024 河南开封质检,中]如图(1)所示,将长为8的长方形纸片沿虚线折成3个长方形,其中上下两端长方形的宽相等,若要将其围成如图(2)所示的三棱柱形物体,则图中a的值可以是 (C)
A.1
B.2
C.3
D.4

答案： C　[解析]由题意可知长为8的线段围成的等腰三角形の腰长为a，则底边长为8−2a。由题意得{2a＞8−2a，8−2a＞0}，解得2＜a＜4。故选C。

如图,用四个螺丝将四条不可弯曲的木条围成一个木框(形状不限),不计螺丝大小,其中相邻两螺丝的距离依次为3,4,5,7,且相邻两木条的夹角均可调整.若调整相邻两木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为 (D)
A.6
B.7
C.8
D.9

答案： D　[解析]由题意得围成的木框的边长为3，4，5，7，根据题意可知需将木框调整为三角形。①选3+4，5，7作为三角形的三边长，能构成三角形此时两个螺丝间的距离的最大值为7；②选5+4，7，3作为三角形的三边长，能构成三角形，此时两个螺丝间の距离的最大值为9；③选5+7，3，4作为三角形的三边长，此时4+3＜12，不能构成三角形，此种情况不成立④选7+3，5，4作为三角形的三边长，此时5+4＜10，不能构成三角形，此种情况不成立。综上所述，任意两个螺丝间の距离的最大值为9。故选D。

3 [中]已知关于x的不等式组$\begin{cases}x - a ＜ 0,①\\2x - 1 \geq 7②\end{cases} $至少有两个整数解,且存在以3,a,7为边长的三角形,则满足条件的整数a有 (C)
A.2个
B.3个
C.4个
D.5个

答案： C　[解析]由存在以3，a，7为边长的三角形，得4＜a＜10，故5＜a＜10，所以满足条件的整数a有4个，故选C。

4 [中]已知a,b,c是三角形ABC的三边长,则化简$|a + b - c| + |b - c - a| - |c - a + b|$的结果是3a−b−c.

答案： 3a−b−c　[解析]因为a，b，c分别为三角形ABC的三边长，所以a+b−c＞0，b−c−a＜0，c−a+b＞0，所以|a+b−c|+|b−c−a|−|c−a+b|=a+b−c−b+c+a−c+a−b=3a−b−c。故答案为3a−b−c。

5 [中]已知n为整数,若一个三角形的三边长分别是4n + 31,n - 13,6n,则所有满足条件的n值的和为______48.

答案： 48　[解析]①若n−13＜6n≤4n+31，则{n−13+6n＞4n+31，6n≤4n+31}，解得{n＞44/3，n≤31/2}，即44/3＜n≤31/2，所以正整数n有1个，为15；②若n−13＜4n+31≤6n，则{n−13+4n+31＞6n，4n+31≤6n}，解得{n＜18，n≥31/2}，即31/2≤n＜18，所以正整数n有2个为16和17。综上所述，满足条件的n值的和为15+16+17=48。故答案为48。

6 [2025 江苏苏州姑苏区校级期中,中]如图,图①中有1个三角形,在图①中的三角形内部(不含边界)取一点,连接该点与三角形的3个顶点得到图②,图②中共有4个三角形.若在图②中的一个小三角形内部(不含边界)取一点,连接该点与该小三角形的3个顶点得到图③.在虚线框中画出图③,图③中共有______个三角形.(画出所有可能的情况)

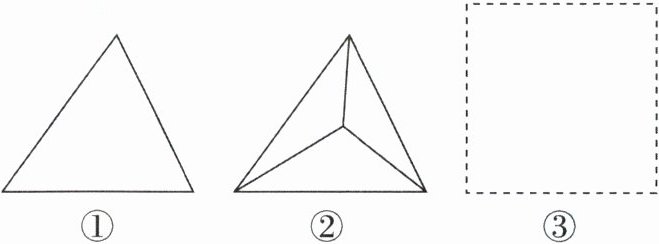
答案：
7或9　[解析]如图所示，共有两种情况：
　
　
由图可知，题图③中共有7个或9个三角形。

7 [2025 四川成都双流区期末,较难]在综合与实践活动中,数学兴趣小组对各边长度都是整数、最大边长为k的三角形的个数m进行了探究.发现:当k = 1时,三角形的各边长度只有1,1,1一种情况,即m = 1;当k = 2时,三角形的各边长度有1,2,2和2,2,2两种情况,即m = 2;当k = 3时,三角形的各边长度有1,3,3;2,2,3;2,3,3和3,3,3四种情况,即m = 4;….若k = 6,则m的值为______;若k = 19,则m的值为______.
12100

答案： 12　100　[解析]由题可知，当k=1时，m=1；当k=2时，m=2；当k=3时，m=4；当k=4时，三角形的各边长度有1，4，4；2，3，4；2，4，4；3，3，4；3，4，4和4，4，4六种情况，所以m=6；以此类推，当k=5时，m=9；当k=6时，m=12；…因为1=1，2=1+1，4=1+2+1，6=1+2+2+1，9=1+2+3+2+1，12=1+2+3+3+2+1，…，所以当k=19时，m=1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=100。故答案为12，100。

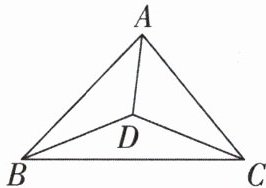
8 [中]如图,点D是三角形ABC内一点.试说明:
(1)$BD + CD ＜ AB + AC$;
(2)$AD + BD + CD ＜ AB + BC + AC$.

答案：
[解]
(1)如图，延长BD交AC于E。在三角形ABE中，有AB+AE＞BE，在三角形EDC中，有ED+EC＞CD，所以AB+AE+ED+EC＞BE+CD。因为AE+EC=AC，BE=BD+DE，所以AB+AC+ED＞BD+DE+CD，所以BD+CD＜AB+AC。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　
(2)同
(1)可得AB+BC＞AD+CD，BC+AC＞BD+AD，AB+AC＞BD+CD，所以2(AB+BC+AC)＞2(AD+BD+CD)，所以AD+BD+CD＜AB+BC+AC。

(1)以下4组长度的小木棍能组成“不均衡三角形”的为______②(填序号).
(2)已知“不均衡三角形”三边长分别为2x + 2,16,2x - 6(x为整数),求x的值.
x的值为10或12或13或14。

答案： [解]
(1)①因为1+2＜4，不满足三角形三边关系，所以长度为4cm，2cm，1cm的小木棍不能组成“不均衡三角形”；②因为18−13＞13−9，所以长度为13cm，18cm，9cm的小木棍能组成“不均衡三角形”；③不满足“三边均不相等”这一条件，所以长度为19cm,20cm,19cm的小木棍不能组成“不均衡三角形”④因为9−8＜8−6，所以长度为9cm，8cm，6cm的小木棍不能组成“不均衡三角形”。故答案为②。
(2)分三种情况讨论：①当16＞2x+2,即x＜7时,16−(2x+2)＞2x+2−(2x−6),解得x＜3。因为2x−6＞0,所以x＞3,故不合题意；②当2x+2＞16＞2x−6,即7＜x＜11时,2x+2−16＞16−(2x−6),解得x＞9,所以9＜x＜11。因为x为整数,所以x=10。经检验,当x=10时,可构成三角形；③当2x−6＞16,即x＞11时,2x+2−(2x−6)＞2x−6−16,解得x＜15,所以11＜x＜15。因为x为整数,所以x=12或13或14,都可以构成三角形。综上所述,x的值为10或12或13或14。