第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 已知一元一次方程$kx + b = 0的解是x = 3$,则函数$y = kx + b$的图象可能是 (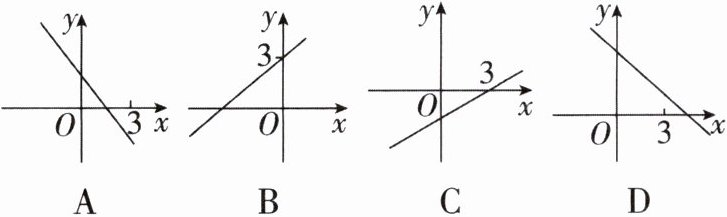
C
)
答案:
C【解析】因为一元一次方程kx+b=0的解是x=3,所以y=kx+b的图象经过点(3,0).故选C.
2 [2024 安徽蚌埠蚌山区质检]一次函数$y = ax + b中的自变量x与函数y$的对应值如下表所示:
| $x$ | …$$ | $-1$ | $0$ | …$$ |
| $y$ | …$$ | $-\pi$ | $1$ | …$$ |
则关于$x的方程ax + b = 0$的解满足 ( )
A.$x < 1$
B.$-1 < x < 0$
C.$0 < x < 1$
D.$x > 1$
| $x$ | …$$ | $-1$ | $0$ | …$$ |
| $y$ | …$$ | $-\pi$ | $1$ | …$$ |
则关于$x的方程ax + b = 0$的解满足 ( )
A.$x < 1$
B.$-1 < x < 0$
C.$0 < x < 1$
D.$x > 1$
答案:
B【解析】因为当x=-1时,y=-π;当x=0时,y=1,所以当-1<x<0时,y的值由负到正,函数图象如图所示,所以关于x的方程ax+b=0的解满足-1<x<0.故选B.

B【解析】因为当x=-1时,y=-π;当x=0时,y=1,所以当-1<x<0时,y的值由负到正,函数图象如图所示,所以关于x的方程ax+b=0的解满足-1<x<0.故选B.

如图,一次函数$y = kx + b(k < 0)的图象经过点A$,则方程$kx + b = 3$的解是 (
A.$x = b$
B.$x = 2$
C.$x = 3$
D.$x = -\frac{b}{x}$
B
)A.$x = b$
B.$x = 2$
C.$x = 3$
D.$x = -\frac{b}{x}$
答案:
B【解析】由函数图象可知,当x=2时,y=kx+b=3,所以关于x的方程kx+b=3的解为x=2,故选B.
若$x = 2是关于x的方程mx + n = 0(m \neq 0,n > 0)$的解,则一次函数$y = -m(x - 1) - n的图象与x$轴的交点坐标是
(3,0)
.
答案:
(3,0)【解析】因为方程mx+n=0的解为x=2,所以一次函数y=mx+n的图象与x轴的交点为(2,0),所以一次函数y=-mx-n的图象与x轴的交点为(2,0).因为一次函数y=-mx-n的图象向右平移一个单位长度可得到函数y=-m(x-1)-n的图象,所以一次函数y=-m(x-1)-n的图象与x轴的交点坐标是(3,0).
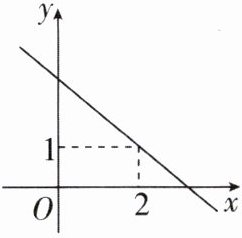
5 [2024 安徽淮北质检]如图,已知一次函数$y = kx + b的图象经过点(2,1)$,则不等式$kx + b - 1 > 0$的解集为 (
A.$x < 2$
B.$x > 2$
C.$x > 1$
D.$x < 1$
A
)
A.$x < 2$
B.$x > 2$
C.$x > 1$
D.$x < 1$
答案:
A【解析】如题图所示,不等式kx+b>1的解集为x<2,所以不等式kx+b-1>0的解集为x<2.故选A.
6 [2025 山东泰安期末]如图,直线$y = kx + b与y = mx + n分别交x轴于点A(-0.5,0)$,$B(2,0)$,则不等式$(kx + b)(mx + n) > 0$的解集为____
-0.5<x<2
.
答案:
-0.5<x<2【解析】因为两个正数或两个负数的积为正数,所以结合图象可知不等式(kx+b)(mx+n)>0的解集为-0.5<x<2,故答案为-0.5<x<2.
7 如图,已知直线$y = ax + b(a,b$为常数,且$a < 0)经过点A(2,1)$,当$ax + b < \frac{1}{2}x$时,$x$的取值范围为____.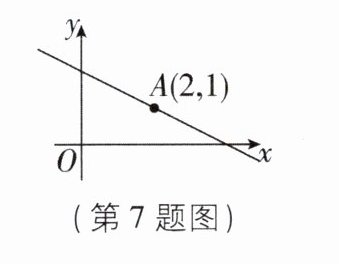

答案:
x>2【解析】如图,因为点A(2,1)也在直线$y=\frac{1}{2}x$上,所以直线$y=\frac{1}{2}x$与直线y=ax+b的交点坐标是A(2,1),所以当$ax+b<\frac{1}{2}x$时,x的取值范围为x>2.故答案是x>2.

x>2【解析】如图,因为点A(2,1)也在直线$y=\frac{1}{2}x$上,所以直线$y=\frac{1}{2}x$与直线y=ax+b的交点坐标是A(2,1),所以当$ax+b<\frac{1}{2}x$时,x的取值范围为x>2.故答案是x>2.

如果一次函数$y = kx + b(k \neq 0)$中两个变量x,y的部分对应值如表所示:
| $x$ | … | $-3$ | $-2$ | $-1$ | $0$ | $1$ | … |
| $y$ | … | $11$ | $8$ | $5$ | $2$ | $-1$ | … |
那么关于$x$的不等式$kx + b \geq 8$的解集是
| $x$ | … | $-3$ | $-2$ | $-1$ | $0$ | $1$ | … |
| $y$ | … | $11$ | $8$ | $5$ | $2$ | $-1$ | … |
那么关于$x$的不等式$kx + b \geq 8$的解集是
x≤-2
.
答案:
x≤-2【解析】根据题表中数据可知函数值y随x的增大而减小,且当x=-2时y=8,所以不等式kx+b≥8的解集是x≤-2.故答案为x≤-2.
9 已知一次函数$y_1 = kx + 2(k$为常数,$k \neq 0)和y_2 = x - 3$.
(1)当$k = -2$时,若$y_1 > y_2$,求$x$的取值范围;
(2)当$x < 1$时,$y_1 > y_2$,结合图象,直接写出$k$的取值范围.
(1)当$k = -2$时,若$y_1 > y_2$,求$x$的取值范围;
(2)当$x < 1$时,$y_1 > y_2$,结合图象,直接写出$k$的取值范围.
答案:
(1)当k=-2时,$y_1=-2x+2$.根据题意得-2x+2>x-3,解得$x<\frac{5}{3}$.
(2)-4≤k≤1且k≠0.当x=1时,$y_2=x-3=-2$.把(1,-2)代入$y_1=kx+2$得k+2=-2,解得k=-4.结合图象(图象略)可得k的取值范围为-4≤k≤1且k≠0.
(1)当k=-2时,$y_1=-2x+2$.根据题意得-2x+2>x-3,解得$x<\frac{5}{3}$.
(2)-4≤k≤1且k≠0.当x=1时,$y_2=x-3=-2$.把(1,-2)代入$y_1=kx+2$得k+2=-2,解得k=-4.结合图象(图象略)可得k的取值范围为-4≤k≤1且k≠0.
查看更多完整答案,请扫码查看


