《2025年初中必刷题八年级数学上册沪科版》

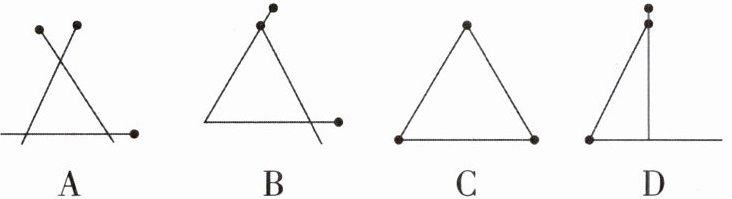
1 下面是小强用三根火柴组成的图形,其中符合三角形概念的是 (C)

答案： C　[解析]因为三角形是由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形，所以C选项符合题意。

如图所示,图中共有4个三角形,它们分别是△ABC，△AEF，△BGE，△GCF.△BGE的三个顶点分别是B，G，E,三条边分别是BE，EG，BG,三个角分别是∠BGE，∠B，∠BEG.

答案： 4　△ABC，△AEF，△BGE，△GCF　B，G，E　BE，EG，BG　∠BGE，∠B，∠BEG　[解析]题图中共有4个三角形，它们分别是△ABC，△AEF，△BGE，△GCF。△BGE的三个顶点分别是B，G，E，三条边分别是BE，EG，BG，三个角分别是∠BGE，∠B，∠BEG。

3 如图表示的是三角形的分类,则下列判断正确的是 (B)
A.M表示三边均不相等的三角形,N表示等腰三角形,P表示等边三角形

B.M表示三边均不相等的三角形,N表示等边三角形,P表示等腰三角形
C.M表示等腰三角形,N表示等边三角形,P表示三边均不相等的三角形
D.M表示等边三角形,N表示等腰三角形,P表示三边均不相等的三角形

答案： B　[解析]三角形根据边长关系分类如下：
三角形{不等边三角形，等腰三角形{底和腰不相等的等腰三角形，等边三角形}
所以M表示三边均不相等的三角形，N表示等边三角形，P表示等腰三角形，故选B。

4 [2025 河南周口校级质检]若使用如图所示的①②两根铁丝做成一个三角形框架,需要将其中一根铁丝折成两段,则可以折成两段的铁丝是 (A)
A.只有①可以
B.只有②可以
C.①②都可以
D.①②都不可以

答案： A　[解析]因为10＞7，所以根据三角形中任意两边的和大于第三边可知，需要将10cm长的铁丝折成两段，即只有①可以，②不可以，故选A。

5 [2024 四川成都校级期中]已知a,b,c是△ABC的三边长,b,c满足$(b - 2)^2 + |c - 3| = 0$,且a为方程$|x - 4| = 2$的解,则△ABC的周长为 ( )

A.4
B.5
C.7或11
D.7

答案：
D　[解析]　

6 [2025 安徽池州期末]若a,b,c为△ABC的三边长,则$(a - b + c)(a - b - c)$＜0(填“＞”“=”或“＜”).

答案： ＜　[解析]因为a，b，c是△ABC的三边长，所以a+c＞b，b+c＞a，所以a−b+c＞0，a−b−c＜0，所以(a−b+c)(a−b−c)＜0，故答案为＜。

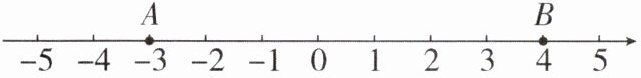
7 新考向开放性试题[2024 安徽滁州期末]如图,数轴上A,B两点到原点的距离是三角形两边的长,则该三角形第三条边的长可能是4(答案不唯一).

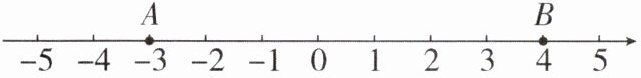
答案： 4(答案不唯一)　[解析]由数轴可得，A到原点的距离为3，B到原点的距离为4。因为数轴上A，B两点到原点的距离是三角形两边的长，所以设该三角形第三条边的长为x，则x的取值范围是1＜x＜7，所以该三角形第三条边的长可能是4(答案不唯一)。

8 已知a,b,c分别为三角形ABC的三边长,且满足$a + b = 3c - 2,a - b = 2c - 6$.
(1)求c的取值范围.
(2)若三角形ABC的周长为12,求c的值.

答案： [解]
(1)因为a，b，c分别为三角形ABC的三边长，a+b=3c−2，a−b=2c−6，所以{3c−2＞c，|2c−6|＜c}解得2＜c＜6。故c的取值范围为2＜c＜6。　　　　　　　　　
(2)因为三角形ABC的周长为12，a+b=3c−2，所以a+b+c=4c−2=12，解得c=3.5。故c的值是3.5。

9 已知等腰三角形的两边长分别为4和10,则这个等腰三角形的周长是______24.

答案： 24　[解析]①若腰长为4，则三角形的三边长分别为4，4，10，而4+4＜10，不符合三角形的三边关系，故腰长不能为4；②若腰长为10，则三角形的三边长分别为10，10，4，且10−4＜10＜10+4，符合三角形的三边关系，此时三角形的周长为24。综上所述，这个等腰三角形的周长为24。