《2025年初中必刷题八年级数学上册沪科版》

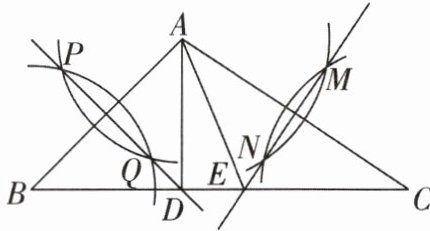
1 [2025 安徽合肥期末,中]如图,在△ABC 中,分别以 A,B 为圆心,大于 $\frac{1}{2}AB$ 的长为半径画弧,两弧交于 P,Q 两点,作直线 PQ 交 BC 于点 D,连接 AD. 再分别以 A,C 为圆心,大于 $\frac{1}{2}AC$ 的长为半径画弧,两弧交于 M,N 两点,作直线 MN 交 BC 于点 E,连接 AE. 若 CD = 11,且△ADE 的周长为 17,则 BD 的长为(C)

A.4
B.5
C.6
D.7

答案： C 【解析】由作图过程得 PQ 垂直平分 AB，MN 垂直平分 AC，
∴ DA=DB，EA=EC.
∵ △ADE 的周长为 17，
∴ AD+DE+AE=17，
∴ DB+DE+EC=17，即 DB+CD=17，
∴ BD+11=17，
∴ BD=6. 故选 C.

2 [较难]如图,已知 AD 是△ABC 的角平分线,AD 的垂直平分线交 AB 于点 F,交 BC 的延长线于点 E,连接 FD,AE. 以下四个结论：(1)∠EAD = ∠EDA；(2)DF // AC；(3)∠FDE = 90°；(4)∠B = ∠CAE. 其中恒成立的结论有( )


A.(1)(2)
B.(2)(3)(4)
C.(1)(2)(4)
D.(1)(2)(3)(4)

答案：
C 【解析】设 AD 与 EF 交于点 O，如图所示.

由以上可知
(1)
(2)恒成立.
∵ FD 与 BE 不一定互相垂直，
∴
(3)∠FDE=90°不一定成立.由
(1)
(2)知∠EAD=∠EDA，∠FAD=∠CAD.

故
(4)恒成立.

3 [中]已知 C,D 两点在线段 AB 的垂直平分线上,且 ∠ACB = 50°,∠ADB = 86°,则 ∠CAD 的度数是______。

答案：
18°或 112° 【解析】如图，
∵ C，D 两点在线段 AB 的垂直平分线上，
∴ CA=CB，DA=DB，CD⊥AB，
∴ 易证△AOC≌△BOC，△ADO≌△BDO，
∴ ∠ACD=∠BCD=1/2∠ACB=1/2×50°=25°，∠ADO=∠BDO=1/2∠ADB=1/2×86°=43°. 当点 C 与点 D 在线段 AB 两侧时，∠CAD=180°-∠ACD-∠ADC=180°-25°-43°=112°；当点 C 与点 D'在线段 AB 同侧时，∠CAD'=∠AD'O-∠ACD'=43°-25°=18°. 故答案为 18°或 112°.

4 [2025 湖南邵阳期末,中]如图,直线 m 是△ABC 中 BC 边的垂直平分线,点 P 是直线 m 上的一动点. 若 AB = 6,AC = 4,BC = 7,则△APC 周长的最小值是______。

答案：
10 【解析】如图，连接 PB.
∵ 直线 m 垂直平分 BC，
∴ BP=CP.
∵ AP+BP≥AB，
∴ AP+BP 的最小值为 AB 的长，即 AP+CP 的最小值为 AB 的长，
∴ △APC 周长的最小值是 6+4=10. 故答案为 10.

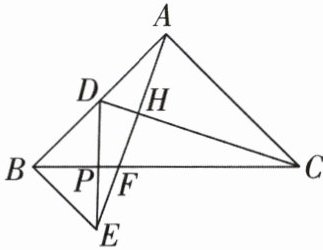
5 [2024 安徽无为期中,难]如图,在 Rt△ABC 中,∠BAC = 90°,AB = AC,点 D 是 AB 的中点,AF ⊥ CD 于 H,交 BC 于 F,BE // AC 交 AF 的延长线于 E,连接 DE 交 BC 于 P. 求证：
(1)△ABE ≌ △CAD；
(2)BC 垂直平分 DE.

答案： 【证明】
(1)由题意可知，∠BAC=∠AHD=90°，
∴ ∠DAH+∠ADH=90°，∠ACH+∠ADH=90°，
∴ ∠DAH=∠ACH.
∵ ∠BAC=90°，BE//AC，
∴ ∠CAD=∠ABE=90°. 在△ABE 与△CAD 中，{∠DAH=∠ACH，AB=AC，∠ABE=∠CAD}，
∴ △ABE≌△CAD(ASA).
(2)
∵ △ABE≌△CAD，
∴ AD=BE. 又
∵ AD=BD，
∴ BD=BE. 在 Rt△ABC 中，∠BAC=90°，AB=AC，
∴ ∠ABC=45°.
∵ ∠ABE=90°，
∴ ∠EBF=90°-45°=45°，
∴ ∠ABC=∠EBF.
∵ BP=BP，
∴ △DBP≌△EBP(SAS)，
∴ DP=EP，∠DPB=∠EPB=90°，
∴ BC 垂直平分 DE.

6 核心素养 推理能力 [难]如图,在四边形 ABCD 中,∠A = ∠B = 90°,AB = 25 cm,DA = 15 cm,CB = 10 cm. 动点 E 沿 AB 边从点 A 出发,以 2 cm/s 的速度向点 B 移动,设移动的时间为 x s.
(1)当 x 为何值时,点 E 在线段 CD 的垂直平分线上？
(2)在(1)的条件下,判断 DE 与 CE 的位置关系,并说明理由。

答案： 【解】
(1)当 x=5 时，点 E 在线段 CD 的垂直平分线上.当 x=5 时，AE=2×5=10(cm).
∵ AB=25 cm，DA=15 cm，CB=10 cm，
∴ BE=AB-AE=15 cm=DA，AE=CB.在△ADE 和△BEC 中，{AD=BE，∠A=∠B，AE=BC}，
∴ △ADE≌△BEC(SAS)，
∴ DE=CE，
∴ 点 E 在线段 CD 的垂直平分线上. 即当 x=5 时，点 E 在线段 CD 的垂直平分线上.
(2)DE 与 CE 的位置关系是 DE⊥CE.理由：
∵ △ADE≌△BEC，
∴ ∠ADE=∠CEB.
∵ ∠A=90°，
∴ ∠ADE+∠AED=90°，
∴ ∠AED+∠CEB=90°，
∴ ∠DEC=180°-(∠AED+∠CEB)=90°，
∴ DE⊥CE.