《2025年初中必刷题八年级数学上册沪科版》

一、选择题(共 45 分)
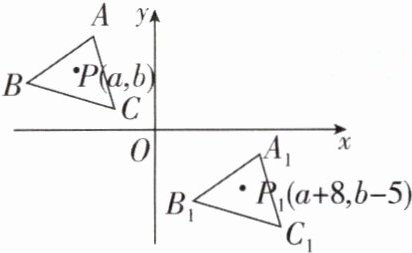
1 [2025 安徽六安裕安区质检]如图,在平面直角坐标系中,将三角形$ABC平移至三角形A_{1}B_{1}C_{1}$的位置,点$P(a,b)是三角形ABC$内一点,经平移后得到三角形$A_{1}B_{1}C_{1}内对应点P_{1}(a + 8,b - 5)$,若点$A_{1}的坐标为(5,-1)$,则点$A$的坐标为 (D)

A.$(-4,3)$
B.$(-1,2)$
C.$(-6,2)$
D.$(-3,4)$

答案： D 【解析】因为点$P(a,b)$是三角形$ABC$内一点，经平移后得到三角形$A_1B_1C_1$内对应点$P_1(a + 8,b - 5)$，点$A_1$的坐标为$(5,-1)$，所以设$A(x,y)$，则$x + 8 = 5$，$y - 5 = - 1$，解得$x = - 3$，$y = 4$，所以$A(-3,4)$。故选D。

如图,在平面直角坐标系中,动点$A从(1,0)$出发,向上运动 1 个单位长度到达点$B(1,1)$,分裂为两个点,分别向左、右运动到点$C(0,2)$,点$D(2,2)$,此时称动点$A$完成第一次跳跃,再分别从$C,D$点出发,每个点重复之前的运动,到达点$G(-1,4)$,$H(1,4)$,$I(3,4)$,此时称动点$A$完成第二次跳跃,以此规律跳跃下去,动点$A$完成第 2023 次跳跃时,从右往左数的第二个点的坐标是 (C)
A.$(2023,4044)$
B.$(2024,4046)$
C.$(2022,4046)$
D.$(2020,4044)$

答案： C 【解析】由题意可得，每完成一次跳跃，到达点的纵坐标增加2，到达最右边的点的横坐标增加1，则动点$A$完成第2023次跳跃时，所有到达点的纵坐标为$2023×2 = 4046$，最右边的点的横坐标为$1 + 2023 = 2024$，则从右往左数的第二个点的坐标是$(2022,4046)$。故选C。

3 新考法 [2024 北京密云区期末]在平面直角坐标系$xOy$中,点$A(2,1)$,$B(b,0)$,$C(4 - b,0)$,其中点$B在点C$左侧. 连接$AB,AC$,若在$AB,AC,BC$所围成的区域内(含边界),横坐标和纵坐标都为整数的点的个数为 6,则$b$的取值范围是 ( )

A.$-1 ＜ b \leq 0$
B.$-1 \leq b ＜ 0$
C.$0 \leq b ＜ 1$
D.$0 ＜ b \leq 1$

答案：
A 【解析】因为点$B(b,0)$在点$C(4 - b,0)$的左侧，所以$b ＜ 4 - b$，解得$b ＜ 2$。记边$AB$，$AC$，$BC$所围成的区域（含边界）为区域$M$，则落在区域$M$的横、纵坐标都为整数的点的个数为6。因为点$A(2,1)$，$B(b,0)$，$C(4 - b,0)$，所以区域$M$的内部（不含边界）没有横、纵坐标都为整数的点，所以6个横、纵坐标都为整数的点都在区域$M$的边界上。因为点$A(2,1)$的横、纵坐标都为整数且在区域$M$的边界上，所以其他的5个点都在线段$BC$上，如图，所以$4\leq4 - b ＜ 5$，解得$-1 ＜ b\leq0$。故选A。

二、填空题(共 30 分)
4 [2025 陕西咸阳期中]在平面直角坐标系中,若点$A(-2,6)与点B(x,y)在同一条平行于x$轴的直线上,且点$B到y$轴的距离为 7,则点$B$的坐标为(7,6)或(-7,6).

答案： (7,6)或$(-7,6)$ 【解析】因为点$A(-2,6)$与点$B(x,y)$在同一条平行于$x$轴的直线上，所以$y = 6$。因为点$B$到$y$轴的距离为7，所以$x = 7$或$x = - 7$，所以点$B$的坐标为$(7,6)$或$(-7,6)$。故答案为$(7,6)$或$(-7,6)$。

5 [2025 安徽阜阳质检]如图,在平面直角坐标系中,线段$AB经过原点O$,$A(2,m)$,$B(-3,n)$,$C(0,-2)$,$CD \perp AB于点D$. 若$AB = 8$,则线段$CD$的长为$\frac{5}{4}$.

答案： $\frac{5}{4}$ 【解析】由题意可得$S_{\triangle ABC}=\frac{1}{2}× AB× CD=\frac{1}{2}× OC×[2 - (-3)]$，$\frac{1}{2}×8× CD=\frac{1}{2}×2×[2 - (-3)]$，解得$CD = \frac{5}{4}$。故答案为$\frac{5}{4}$。

6 [2024 安徽铜陵铜官区期末]【问题情境】
我们知道:在平面直角坐标系中有不重合的两点$A(x_{1},y_{1})和B(x_{2},y_{2})$,若$x_{1} = x_{2}$,则$AB // y$轴,且线段$AB的长度为|y_{1} - y_{2}|$;若$y_{1} = y_{2}$,则$AB // x$轴,且线段$AB的长度为|x_{1} - x_{2}|$.
【拓展】
现在,若规定:平面直角坐标系中任意不重合的两点$M(x_{1},y_{1})$,$N(x_{2},y_{2})之间的折线距离为d(M,N) = |x_{1} - x_{2}| + |y_{1} - y_{2}|$. 例如:图中,点$M(-1,1)与点N(1,-2)之间的折线距离d(M,N) = |-1 - 1| + |1 - (-2)| = 2 + 3 = 5$.
【应用】解决下列问题:
(1)已知点$E(3,2)$,点$F(1,-2)$,求$d(E,F)$的值.
(2)已知点$G(3,1)$,$H(-1,n)$,若$d(G,H) = 6$,直接写出$n$的值.
(3)已知点$P(3,4)$,点$Q在y$轴上,$O$为坐标系原点,且$\triangle OPQ$的面积是 4.5,求$d(P,Q)$的值.

答案：
【解】
(1)因为点$E(3,2)$，点$F(1,-2)$，所以$d(E,F)=|3 - 1|+|2 - (-2)| = 6$。
(2)$n = - 1$或$n = 3$。因为$G(3,1)$，$H(-1,n)$，$d(G,H)=6$，所以$d(G,H)=|3 - (-1)|+|1 - n| = 6$，解得$n = - 1$或$n = 3$。
(3)设$Q(0,m)$。由题意，得$\frac{1}{2}\cdot|m|\cdot3 = 4.5$，解得$m = \pm3$，所以点$Q$的坐标为$(0,3)$或$(0,-3)$。如图，当点$Q$的坐标为$(0,3)$时，$d(P,Q)=|3 - 0|+|4 - 3| = 4$；当点$Q'$的坐标为$(0,-3)$时，$d(P,Q')=|3 - 0|+|4 - (-3)| = 10$。综上，$d(P,Q)$的值为4或10。