2025年暑假大串联七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假大串联七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
22. 如图,已知线段$AB=8cm$,$C$是线段$AB$上一点,$AC=3cm$,$M$是$AB$的中点,$N$是$AC$的中点.
(1)求线段$CM$的长;
(2)求线段$MN$的长.

(1)求线段$CM$的长;
1cm
(2)求线段$MN$的长.
2.5cm

答案:
(1) $\because AB = 8cm$, M 是 AB 的中点, $\therefore AM = \frac{1}{2}AB = 4cm$. $\because AC = 3cm, \therefore CM = AM - AC = 4cm - 3cm = 1cm$;
(2) $\because AB = 8cm, AC = 3cm$, M 是 AB 的中点, N 是 AC 的中点, $\therefore AM = \frac{1}{2}AB = 4cm, AN = \frac{1}{2}AC = 1.5cm, \therefore MN = AM - AN = 4cm - 1.5cm = 2.5cm$.
(1) $\because AB = 8cm$, M 是 AB 的中点, $\therefore AM = \frac{1}{2}AB = 4cm$. $\because AC = 3cm, \therefore CM = AM - AC = 4cm - 3cm = 1cm$;
(2) $\because AB = 8cm, AC = 3cm$, M 是 AB 的中点, N 是 AC 的中点, $\therefore AM = \frac{1}{2}AB = 4cm, AN = \frac{1}{2}AC = 1.5cm, \therefore MN = AM - AN = 4cm - 1.5cm = 2.5cm$.
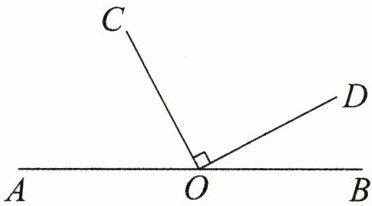
23. 定义:从$∠α(90^{\circ}<α<180^{\circ})$的顶点出发,在角的内部作一条射线,若该射线将$∠α$分得的两个角中有一个角与$∠α$互为补角,则称该射线为$∠α$的“好线”.如图,点$O$在直线$AB$上,$OC$,$OD$在直线$AB$上方,且$OC⊥OD$,射线$OE$是$∠AOD$的“好线”.
(1)若$∠BOD=26^{\circ}$,且$OE$在$∠COD$内部,则$∠COE=$______$^{\circ}$;
(2)若$OE$恰好平分$∠AOC$,请求出$∠BOD$的度数;
(3)若$OF$是$∠AOE$的平分线,$OG$是$∠BOC$的平分线,请画出图形,探究$∠EOF$与$∠DOG$的数量关系,并说明理由.
(1)若$∠BOD=26^{\circ}$,且$OE$在$∠COD$内部,则$∠COE=$______$^{\circ}$;
(2)若$OE$恰好平分$∠AOC$,请求出$∠BOD$的度数;
(3)若$OF$是$∠AOE$的平分线,$OG$是$∠BOC$的平分线,请画出图形,探究$∠EOF$与$∠DOG$的数量关系,并说明理由.

答案:
(1) 如图,
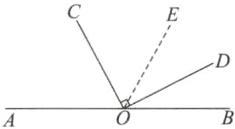
$\because$ 射线 OE 是 $\angle AOD$ 的“好线”, $\therefore \angle AOD + \angle DOE = 180^{\circ}, \because \angle AOD + \angle BOD = 180^{\circ}$,
$\therefore \angle DOE = \angle BOD = 26^{\circ}, \because OC \perp OD$,
$\therefore \angle COD = 90^{\circ}, \therefore \angle COE = \angle COD - \angle DOE = 90^{\circ} - 26^{\circ} = 64^{\circ}$, 故答案为 64;
(2) 如图, OE 平分 $\angle AOC$,

$\because$ 射线 OE 是 $\angle AOD$ 的“好线”, $\therefore \angle AOE + \angle AOD = 180^{\circ}, \because \angle AOD + \angle BOD = 180^{\circ}$,
$\therefore \angle AOE = \angle BOD, \because OE$ 恰好平分 $\angle AOC$,
$\therefore \angle AOE = \angle COE = \angle BOD, \because \angle AOE + \angle COE + \angle COD + \angle BOD = 180^{\circ}, \therefore 90^{\circ} + 3\angle BOD = 180^{\circ}, \therefore \angle BOD = 30^{\circ}$;
(3) $\angle EOF = 2\angle DOG$ 或 $\angle EOF + \angle DOG = 45^{\circ}$.
理由: ① 当 OE 在 $\angle COD$ 内部时, 如图,

由
(1) 可得, $\angle DOE = \angle BOD$, 设 $\angle DOE = \angle BOD = x$, 则 $\angle AOE = 180^{\circ} - 2x, \angle BOC = 90^{\circ} + x, \because OF$ 是 $\angle AOE$ 的平分线, OG 是 $\angle BOC$ 的平分线, $\therefore \angle EOF = \frac{1}{2}\angle AOE = \frac{1}{2}(180^{\circ} - 2x) = 90^{\circ} - x, \angle BOG = \frac{1}{2}\angle BOC = \frac{1}{2}(90^{\circ} + x), \therefore \angle DOG = \angle BOG - \angle BOD = \frac{1}{2}(90^{\circ} + x) - x = \frac{1}{2}(90^{\circ} - x), \therefore \angle EOF = 2\angle DOG$;
② 当 OE 在 $\angle AOC$ 内部时, 如图,
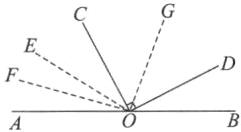
由
(2) 可得 $\angle AOE = \angle BOD$, 设 $\angle AOE = \angle BOD = x$, 则 $\angle BOC = 90^{\circ} + x, \because OF$ 是 $\angle AOE$ 的平分线, OG 是 $\angle BOC$ 的平分线,
$\therefore \angle EOF = \frac{1}{2}\angle AOE = \frac{1}{2}x, \angle BOG = \frac{1}{2}\angle BOC = \frac{1}{2}(90^{\circ} + x), \therefore \angle DOG = \angle BOG - \angle BOD = \frac{1}{2}(90^{\circ} + x) - x = 45^{\circ} - \frac{1}{2}x, \therefore \angle EOF + \angle DOG = \frac{1}{2}x + 45^{\circ} - \frac{1}{2}x = 45^{\circ}$; 综上, 当 OE 在 $\angle COD$ 内部时, $\angle EOF = 2\angle DOG$; 当 OE 在 $\angle AOC$ 内部时, $\angle EOF + \angle DOG = 45^{\circ}$.
(1) 如图,

$\because$ 射线 OE 是 $\angle AOD$ 的“好线”, $\therefore \angle AOD + \angle DOE = 180^{\circ}, \because \angle AOD + \angle BOD = 180^{\circ}$,
$\therefore \angle DOE = \angle BOD = 26^{\circ}, \because OC \perp OD$,
$\therefore \angle COD = 90^{\circ}, \therefore \angle COE = \angle COD - \angle DOE = 90^{\circ} - 26^{\circ} = 64^{\circ}$, 故答案为 64;
(2) 如图, OE 平分 $\angle AOC$,

$\because$ 射线 OE 是 $\angle AOD$ 的“好线”, $\therefore \angle AOE + \angle AOD = 180^{\circ}, \because \angle AOD + \angle BOD = 180^{\circ}$,
$\therefore \angle AOE = \angle BOD, \because OE$ 恰好平分 $\angle AOC$,
$\therefore \angle AOE = \angle COE = \angle BOD, \because \angle AOE + \angle COE + \angle COD + \angle BOD = 180^{\circ}, \therefore 90^{\circ} + 3\angle BOD = 180^{\circ}, \therefore \angle BOD = 30^{\circ}$;
(3) $\angle EOF = 2\angle DOG$ 或 $\angle EOF + \angle DOG = 45^{\circ}$.
理由: ① 当 OE 在 $\angle COD$ 内部时, 如图,

由
(1) 可得, $\angle DOE = \angle BOD$, 设 $\angle DOE = \angle BOD = x$, 则 $\angle AOE = 180^{\circ} - 2x, \angle BOC = 90^{\circ} + x, \because OF$ 是 $\angle AOE$ 的平分线, OG 是 $\angle BOC$ 的平分线, $\therefore \angle EOF = \frac{1}{2}\angle AOE = \frac{1}{2}(180^{\circ} - 2x) = 90^{\circ} - x, \angle BOG = \frac{1}{2}\angle BOC = \frac{1}{2}(90^{\circ} + x), \therefore \angle DOG = \angle BOG - \angle BOD = \frac{1}{2}(90^{\circ} + x) - x = \frac{1}{2}(90^{\circ} - x), \therefore \angle EOF = 2\angle DOG$;
② 当 OE 在 $\angle AOC$ 内部时, 如图,

由
(2) 可得 $\angle AOE = \angle BOD$, 设 $\angle AOE = \angle BOD = x$, 则 $\angle BOC = 90^{\circ} + x, \because OF$ 是 $\angle AOE$ 的平分线, OG 是 $\angle BOC$ 的平分线,
$\therefore \angle EOF = \frac{1}{2}\angle AOE = \frac{1}{2}x, \angle BOG = \frac{1}{2}\angle BOC = \frac{1}{2}(90^{\circ} + x), \therefore \angle DOG = \angle BOG - \angle BOD = \frac{1}{2}(90^{\circ} + x) - x = 45^{\circ} - \frac{1}{2}x, \therefore \angle EOF + \angle DOG = \frac{1}{2}x + 45^{\circ} - \frac{1}{2}x = 45^{\circ}$; 综上, 当 OE 在 $\angle COD$ 内部时, $\angle EOF = 2\angle DOG$; 当 OE 在 $\angle AOC$ 内部时, $\angle EOF + \angle DOG = 45^{\circ}$.
24. 川美佳超市经销甲、乙两种商品,两种商品相关信息如下表:
|商品|进价(元/件)|售价(元/件)|利润率|
|----|----|----|----|
|甲种|40|60|$n$|
|乙种|50|$m$|50%|
(1)以上表格中$m$,$n$的值分别为
(2)若该超市同时购进甲种商品数量是乙种商品数量的2倍少10件,且在正常销售情况下售完这两种商品共获利3050元,求购进甲、乙两种商品各多少件?
购进甲种商品
(3)春节临近,该超市决定对甲、乙两种商品进行如下的优惠活动:
|顾客一次性购商品|数量|优惠措施|
|----|----|----|
|甲种|不超过15件|不优惠|
| |超过15件|全部按售价8.5折|
|乙种|不超过15|不优惠|
| |超过15件但不超过25件|全部按售价8.8折|
| |超过25件|全部按售价8折|
小华的爸爸一次性购包含甲、乙两种商品共40件,按上述条件优惠后实付款恰好为2280元,求出小华的爸爸购买方案.
方案1:购买甲种商品
|商品|进价(元/件)|售价(元/件)|利润率|
|----|----|----|----|
|甲种|40|60|$n$|
|乙种|50|$m$|50%|
(1)以上表格中$m$,$n$的值分别为
75
、50%
;(2)若该超市同时购进甲种商品数量是乙种商品数量的2倍少10件,且在正常销售情况下售完这两种商品共获利3050元,求购进甲、乙两种商品各多少件?
购进甲种商品
90
件,乙种商品50
件;(3)春节临近,该超市决定对甲、乙两种商品进行如下的优惠活动:
|顾客一次性购商品|数量|优惠措施|
|----|----|----|
|甲种|不超过15件|不优惠|
| |超过15件|全部按售价8.5折|
|乙种|不超过15|不优惠|
| |超过15件但不超过25件|全部按售价8.8折|
| |超过25件|全部按售价8折|
小华的爸爸一次性购包含甲、乙两种商品共40件,按上述条件优惠后实付款恰好为2280元,求出小华的爸爸购买方案.
方案1:购买甲种商品
24
件,乙种商品16
件;方案2:购买甲种商品30
件,乙种商品10
件.
答案:
(1) 根据题意得 $n = \frac{60 - 40}{40}×100\% = 50\%$;
$\frac{m - 50}{50}×100\% = 50\%$, 解得 $m = 75$;
(2) 设购进乙种商品 $x$ 件, 则购进甲种商品 $(2x - 10)$ 件,
根据题意得 $(60 - 40)(2x - 10) + (75 - 50)x = 3050$, 解得 $x = 50, \therefore 2x - 10 = 2×50 - 10 = 90$
(件). 所以购进甲种商品 90 件, 乙种商品 50 件;
(3) 设购买甲种商品 $y$ 件, 则购买乙种商品 $(40 - y)$ 件. 当 $0 < y < 15$ 时, $60y + 75×0.8(40 - y) = 2400 ≠ 2280$, 不符合题意, 舍去; 当 $y = 15$ 时, $60×15 + 75×0.88×(40 - 15) = 2550 ≠ 2280$, 不符合题意, 舍去; 当 $15 < y < 25$ 时, $60×0.85y + 75×0.88(40 - y) = 2280$, 解得 $y = 24$,
$\therefore 40 - y = 40 - 24 = 16$ (件); 当 $y ≥ 25$ 时, $60×0.85y + 75(40 - y) = 2280$, 解得 $y = 30, \therefore 40 - y = 40 - 30 = 10$ (件), $\therefore$ 小华的爸爸共有 2 种购买方案, 方案 1: 购买甲种商品 24 件, 乙种商品 16 件; 方案 2: 购买甲种商品 30 件, 乙种商品 10 件.
(1) 根据题意得 $n = \frac{60 - 40}{40}×100\% = 50\%$;
$\frac{m - 50}{50}×100\% = 50\%$, 解得 $m = 75$;
(2) 设购进乙种商品 $x$ 件, 则购进甲种商品 $(2x - 10)$ 件,
根据题意得 $(60 - 40)(2x - 10) + (75 - 50)x = 3050$, 解得 $x = 50, \therefore 2x - 10 = 2×50 - 10 = 90$
(件). 所以购进甲种商品 90 件, 乙种商品 50 件;
(3) 设购买甲种商品 $y$ 件, 则购买乙种商品 $(40 - y)$ 件. 当 $0 < y < 15$ 时, $60y + 75×0.8(40 - y) = 2400 ≠ 2280$, 不符合题意, 舍去; 当 $y = 15$ 时, $60×15 + 75×0.88×(40 - 15) = 2550 ≠ 2280$, 不符合题意, 舍去; 当 $15 < y < 25$ 时, $60×0.85y + 75×0.88(40 - y) = 2280$, 解得 $y = 24$,
$\therefore 40 - y = 40 - 24 = 16$ (件); 当 $y ≥ 25$ 时, $60×0.85y + 75(40 - y) = 2280$, 解得 $y = 30, \therefore 40 - y = 40 - 30 = 10$ (件), $\therefore$ 小华的爸爸共有 2 种购买方案, 方案 1: 购买甲种商品 24 件, 乙种商品 16 件; 方案 2: 购买甲种商品 30 件, 乙种商品 10 件.
查看更多完整答案,请扫码查看


