《2025年暑假大串联七年级数学人教版》

13. 已知关于$x$，$y$的方程组$\left\{\begin{array}{l} x+my=0,\\ x+y=3\end{array}\right.$的解是$\left\{\begin{array}{l} x=1,\\ y=\otimes,\end{array}\right.$其中$y$的值被盖住了，不过仍能求出$m$的值，则$m$的值是______$ - \frac { 1 } { 2 }$.

答案： $ - \frac { 1 } { 2 }$

14. 如图，长方形木条上有$A$，$B$两点，两点间的距离为$3$个单位长度，当点$A$在数轴上表示的数为$-\sqrt {2}$时，点$B$落在数轴上的点表示的数为$ - \sqrt { 2 } + 3 $或$ - \sqrt { 2 } - 3 $.

答案： $ - \sqrt { 2 } + 3 $或$ - \sqrt { 2 } - 3 $

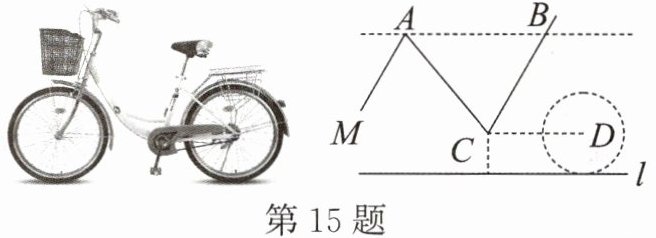
15. 某工厂生产一批某款自行车，这款自行车放在水平地面$l$上的示意图如图所示，$AB// l$，$CD// l$.当$AM// BC$时，自行车是合格产品，若该款自行车质量检验合格，测得$\angle BCD=60^{\circ }$，$\angle BAC=50^{\circ }$，则$\angle MAC=$$70^{\circ }$.

答案： $ 70 ^ { \circ }$

16. 已知关于$x$的不等式组$\left\{\begin{array}{l} 2x-5＜1-x,\\ x-a＞0\end{array}\right.$有且仅有两个整数解，则$a$的取值范围为$-1 \leq a ＜ 0$.

答案： $ - 1 \leq a ＜ 0 $

17. 计算：$\sqrt [3]{27}-\sqrt {25}+|\sqrt {3}-2|$.

答案： $ - \sqrt { 3 }$

18. 求下列各式中$x$的值.
（1）$(x-3)^{3}=-27$；$ x = 0 $
（2）$(x+1)^{2}=16$.$ x = 3 $或$ x = - 5 $

答案：
(1)$ x = 0 $
(2)$ x = 3 $或$ x = - 5 $

19. （1）用代入法解方程组：$\left\{\begin{array}{l} x-2y=-1,\\ 4x+3y=7;\end{array}\right.$
解：$\left\{ \begin{array} { l } { x - 2 y = - 1 , \textcircled { 1 } } \\ { 4 x + 3 y = 7 . \textcircled { 2 } } \end{array} \right.$
由①可得$ x = $$2y - 1$.③
把③代入②，得$4 ( 2 y - 1 ) + 3 y = 7$，解得$ y = $1.
把$ y = 1 $代入③，得$ x = $$2 × 1 - 1$$ = $1.
故方程组的解是$\left\{ \begin{array} { l } { x = 1 , } \\ { y = 1 . } \end{array} \right.$
（2）用加减法解方程组：$\left\{\begin{array}{l} 2x+3y=3,\\ 2x-3y=9.\end{array}\right.$
解：$\left\{ \begin{array} { l } { 2 x + 3 y = 3 , \textcircled { 1 } } \\ { 2 x - 3 y = 9 . \textcircled { 2 } } \end{array} \right.$
由①+②可得$4x = 12$，解得$ x = $3.
把$ x = 3 $代入①，得$2 × 3 + 3 y = 3$，解得$ y = $$-1$.
故方程组的解是$\left\{ \begin{array} { l } { x = 3 , } \\ { y = - 1 . } \end{array} \right.$

答案：
(1)$ \left\{ \begin{array} { l } { x - 2 y = - 1 , \textcircled { 1 } } \\ { 4 x + 3 y = 7 . \textcircled { 2 } } \end{array} \right. $
由①可得$ x = 2 y - 1 $.③
把③代入②，得$ 4 ( 2 y - 1 ) + 3 y = 7 $，解得$ y = 1 $.
把$ y = 1 $代入③，得$ x = 2 \times 1 - 1 = 1 $.
故方程组的解是$ \left\{ \begin{array} { l } { x = 1 , } \\ { y = 1 . } \end{array} \right. $
(2)$ \left\{ \begin{array} { l } { 2 x + 3 y = 3 , \textcircled { 1 } } \\ { 2 x - 3 y = 9 . \textcircled { 2 } } \end{array} \right. $
由①+②可得$ 4 x = 12 $，解得$ x = 3 $.
把$ x = 3 $代入①，得$ 2 \times 3 + 3 y = 3 $，解得$ y = - 1 $.
故方程组的解是$ \left\{ \begin{array} { l } { x = 3 , } \\ { y = - 1 . } \end{array} \right. $

20. 解不等式组：$\left\{\begin{array}{l} 2x+6＞7x-4,\\ \dfrac {4x+2}{5}\geqslant \dfrac {x-1}{2}.\end{array}\right.$

答案： $ \left\{ \begin{array} { l } { 2 x + 6 ＞ 7 x - 4 , \textcircled { 1 } } \\ { \frac { 4 x + 2 } { 5 } \geq \frac { x - 1 } { 2 } . \textcircled { 2 } } \end{array} \right. $
解不等式①，得$ x ＜ 2 $.
解不等式②，得$ x \geq - 3 $.
把不等式①和②的解集在数轴上表示出来，如图所示.
−5−4−3−2−1012345
从图中可以找出两个不等式解集的公共部分，得到不等式组的解集为$ - 3 \leq x ＜ 2 $.