《2025年假日数学吉林出版集团股份有限公司八年级人教版》

11. 物理实验证实：在弹性限度内,某弹簧长度$y(cm)与所挂物体质量x(kg)满足函数关系y= kx+15$. 下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
(1)求$y与x$的函数解析式；$ y = 2x + 15 $
(2)当弹簧长度为20cm时,求所挂物体的质量.所挂物体的质量为 $ 2.5 \, \text{kg} $

答案：
(1) $ y = 2x + 15 $
(2) 所挂物体的质量为 $ 2.5 \, \text{kg} $

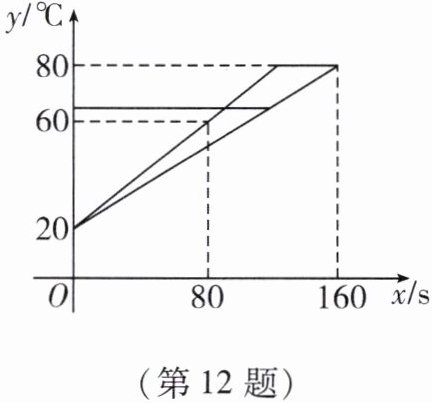
12. 李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快. 在一段时间内,水温$y(^{\circ }C)与加热时间x(s)$之间近似满足一次函数关系,根据记录的数据,画函数图象如下：
(1)加热前水温是20$^{\circ }C$；
(2)求乙壶中水温$y与加热时间x$的函数解析式；
(3)当甲壶中水温刚达到$80^{\circ }C$时,乙壶中水温是65$^{\circ }C$.

答案： 解：
(1) 20
(2) 因为甲壶比乙壶加热速度快，
所以乙壶对应的函数图象经过点 $ (0, 20) $，$ (160, 80) $，
设乙壶中水温 $ y $ 关于加热时间 $ x $ 的函数解析式为 $ y = kx + b (k \neq 0) $，
将点 $ (0, 20) $，$ (160, 80) $ 代入得
$ \begin{cases} 160k + b = 80, \\ b = 20, \end{cases} $ 解得 $ \begin{cases} k = \frac{3}{8}, \\ b = 20, \end{cases} $
则乙壶中水温 $ y $ 关于加热时间 $ x $ 的函数解析式为 $ y = \frac{3}{8}x + 20 $，
自变量 $ x $ 的取值范围是 $ 0 \leq x \leq 160 $。
(3) 65