《2025年假日数学吉林出版集团股份有限公司八年级人教版》

19. 请你观察下面这三个矩形,它们都是由四部分组成的：两个三角形,两个梯形. 但是组合以后,发现它们的面积不一样了,对角线的长也不一样. 这是为什么呢？

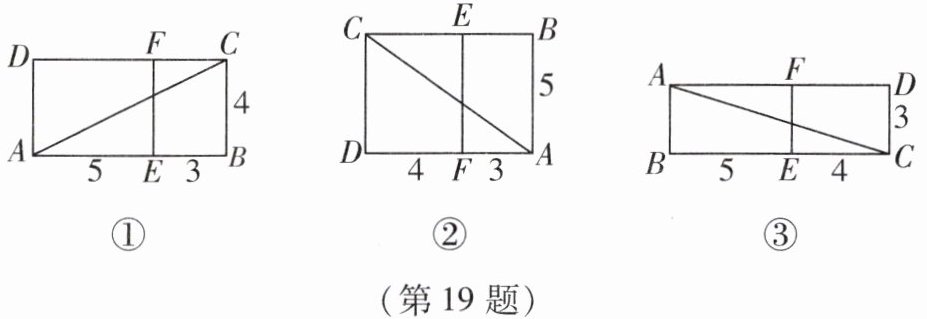
解答：
图①的计算：$AC= \sqrt {4^{2}+8^{2}}= \sqrt {80},S= 4×8= 32$.
图②的计算：$AC= \sqrt {7^{2}+5^{2}}= \sqrt {74},S= 7×5= 35$.
图③的计算：$AC= \sqrt {3^{2}+9^{2}}= \sqrt {90},S= 3×9= 27$.
原来,这四部分看起来相等,实际上是不一样大的,所以组合后面积不相等. 另外,还可以发现,对角线短的反而面积大,对角线长的反而面积小. 想一想,由此可推出什么结论？矩形的面积大小与对角线长短没有必然的大小关系（或不能仅根据对角线长短判断矩形面积大小等合理结论均可）

答案： 【解析】：通过对三个矩形的计算和分析，发现四部分看似相等实则不同，导致组合后面积和对角线长度不同，且存在对角线短面积大、对角线长面积小的现象。
【答案】：矩形的面积大小与对角线长短没有必然的大小关系（或不能仅根据对角线长短判断矩形面积大小等合理结论均可）。