《2025年假日数学吉林出版集团股份有限公司八年级人教版》

14. 图①、图②均为 $4 × 4$ 的正方形网格,每个小正方形的顶点称为格点. 在图①中已画出线段 $AB$,在图②中已画出线段 $CD$,其中 $A$,$B$,$C$,$D$ 均为格点,按下列要求画图：
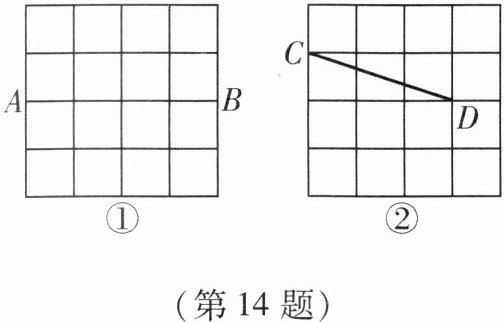
(1) 在图①中,以 $AB$ 为对角线画一个菱形 $AEBF$,且 $E$,$F$ 为格点；
(2) 在图②中,以 $CD$ 为对角线画一个对边不相等的四边形 $CGDH$,且 $G$,$H$ 为格点,$∠CGD = ∠CHD = 90^{\circ}$.

答案： 【解析】：
(1) 菱形的判定方法：一组邻边相等的平行四边形是菱形；对角线互相垂直的平行四边形是菱形；四条边均相等的四边形是菱形。
根据菱形的性质，菱形的对角线互相垂直且平分。
在图①中，先找到$AB$的中点$O$（$AB$横向，中点$O$是格点），然后过$O$点作$AB$的垂线，与格点相交于$E$、$F$点（例如$E$在$A$点正上方一格，$F$在$B$点正上方一格），连接$AE$、$EB$、$BF$、$FA$，则四边形$AEBF$是菱形。
(2) 因为$\angle CGD=\angle CHD = 90^{\circ}$，所以$G$、$H$在以$CD$为直径的圆上（格点中满足条件的点）。
在图②中，$CD$为对角线，先确定$CD$的中点$P$（格点），以$P$为圆心，$\frac{1}{2}CD$长为半径找格点$G$、$H$（例如$G$在$C$点正下方一格，$D$点正左方一格，$H$在$C$点正右方一格，$D$点正上方一格），连接$CG$、$GD$、$DH$、$HC$，得到四边形$CGDH$，且$CG\neq GD$，$DH\neq HC$。
【答案】：
(1) 图①中菱形$AEBF$画法不唯一，示例：$E$在$A$正上方一格，$F$在$B$正上方一格，连接成菱形。
(2) 图②中四边形$CGDH$画法不唯一，示例：$G$在$C$正下方一格，$D$正左方一格；$H$在$C$正右方一格，$D$正上方一格，连接成四边形。

15. 如图,把矩形纸片 $ABCD$ 沿 $EF$ 折叠,使点 $B$ 落在 $AD$ 边上的点 $B'$ 处,点 $A$ 落在点 $A'$ 处.
(1) 求证：$B'E = BF$；
证明：由折叠的性质，得 $BF = B ^ { \prime } F$，$\angle B ^ { \prime } FE = \angle BFE$．又 $\because AD // BC$，$\therefore \angle B ^ { \prime } EF = \angle BFE = \angle B ^ { \prime } FE$．所以 $B ^ { \prime } E = B ^ { \prime } F = BF$．
(2) 设 $AE = a$,$AB = b$,$BF = c$,试猜想 $a$,$b$,$c$ 之间的关系,并给予证明.
猜想：$a ^ { 2 } + b ^ { 2 } = c ^ { 2 }$．
证明：由题意，得 $A ^ { \prime } E = AE = a$，$A ^ { \prime } B ^ { \prime } = AB = b$，$\angle A ^ { \prime } = \angle A = 90 ^ { \circ }$，$\therefore A ^ { \prime } E ^ { 2 } + A ^ { \prime } B ^ { \prime 2 } = B ^ { \prime } E ^ { 2 }$．又 $\because B ^ { \prime } E = BF = c$，$\therefore a ^ { 2 } + b ^ { 2 } = c ^ { 2 }$．

答案：
(1) 由折叠的性质，
得 $BF = B ^ { \prime } F$，$\angle B ^ { \prime } FE = \angle BFE$．
又 $\because AD // BC$，
$\therefore \angle B ^ { \prime } EF = \angle BFE = \angle B ^ { \prime } FE$．
所以 $B ^ { \prime } E = B ^ { \prime } F = BF$．
(2) 猜想：$a ^ { 2 } + b ^ { 2 } = c ^ { 2 }$．
证明：由题意，得 $A ^ { \prime } E = AE = a$，$A ^ { \prime } B ^ { \prime } = AB = b$，$\angle A ^ { \prime } = \angle A = 90 ^ { \circ }$，
$\therefore A ^ { \prime } E ^ { 2 } + A ^ { \prime } B ^ { \prime 2 } = B ^ { \prime } E ^ { 2 }$．
又 $\because B ^ { \prime } E = BF = c$，$\therefore a ^ { 2 } + b ^ { 2 } = c ^ { 2 }$．