《2025年假日数学吉林出版集团股份有限公司八年级人教版》

14. 如图①,圆柱的高为12cm,底面圆的周长为10cm,一只蚂蚁从A点爬到与A点相对的B点处,则需要爬行的最短路径长度是13cm.如图②,圆柱形玻璃杯的高为14cm,底面圆的周长为32cm,在杯内壁距离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正在杯外壁,距离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁点A处到内壁点B处的最短路径长度是20cm(杯壁厚度不计).

答案： 13 20

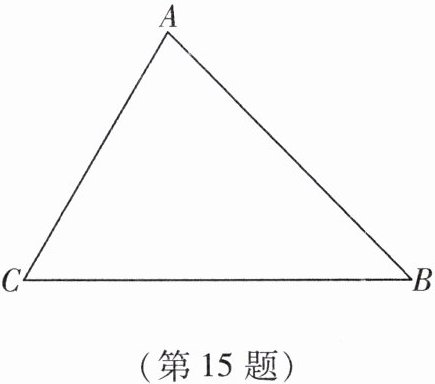
15. 如图,在△ABC中,已知∠C= 60°,AB= 14,AC= 10,求BC的长.

解：根据余弦定理$AB^{2}=AC^{2}+BC^{2}-2AC\cdot BC\cdot\cos C$。
已知$\angle C = 60^{\circ}$，$AB = 14$，$AC = 10$，设$BC=x$，则有：
$14^{2}=10^{2}+x^{2}-2×10x×\cos60^{\circ}$
即$196 = 100 + x^{2}-10x$
移项化为一元二次方程的标准形式：$x^{2}-10x - 96 = 0$
对于一元二次方程$ax^{2}+bx + c = 0$（这里$a = 1$，$b=-10$，$c = -96$），根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$
先计算判别式$\Delta=b^{2}-4ac=(-10)^{2}-4×1×(-96)=100 + 384 = 484$
则$x=\frac{10\pm\sqrt{484}}{2}=\frac{10\pm22}{2}$
$x_{1}=\frac{10 + 22}{2}=16$，$x_{2}=\frac{10-22}{2}=-6$（边长不能为负舍去）
所以$BC$的长为16。

答案： 解：根据余弦定理$AB^{2}=AC^{2}+BC^{2}-2AC\cdot BC\cdot\cos C$。
已知$\angle C = 60^{\circ}$，$AB = 14$，$AC = 10$，设$BC=x$，则有：
$14^{2}=10^{2}+x^{2}-2×10x×\cos60^{\circ}$
即$196 = 100 + x^{2}-10x$
移项化为一元二次方程的标准形式：$x^{2}-10x - 96 = 0$
对于一元二次方程$ax^{2}+bx + c = 0$（这里$a = 1$，$b=-10$，$c = -96$），根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$
先计算判别式$\Delta=b^{2}-4ac=(-10)^{2}-4×1×(-96)=100 + 384 = 484$
则$x=\frac{10\pm\sqrt{484}}{2}=\frac{10\pm22}{2}$
$x_{1}=\frac{10 + 22}{2}=16$，$x_{2}=\frac{10-22}{2}=-6$（边长不能为负舍去）
所以$BC$的长为$16$。