《2025年假日数学吉林出版集团股份有限公司八年级人教版》

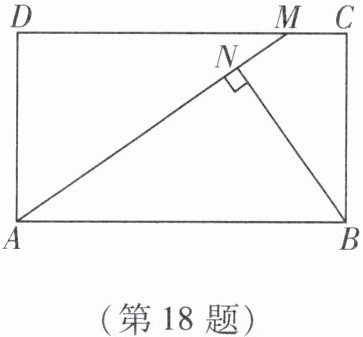
18. 如图,在矩形 $ABCD$ 中,点 $M$ 在 $DC$ 上,$AM = AB$,且 $BN ⊥ AM$,垂足为 $N$.
(1) 求证：$△ABN ≌ △MAD$；
(2) 若 $AD = 2$,$AN = 4$,求四边形 $BCMN$ 的面积.$4\sqrt{5}-8$

答案：
(1) 略
(2) $\because \triangle ABN \cong MAD$，$\therefore BN = AD$．
又 $\because AN = 4$，在 $\mathrm { Rt } \triangle ABN$ 中，
$AB = \sqrt { A N ^ { 2 } + B N ^ { 2 } } = \sqrt { 4 ^ { 2 } + 2 ^ { 2 } } = 2 \sqrt { 5 }$，
$\therefore S _ { \text { 矩形 } A B C D } = 2 × 2 \sqrt { 5 } = 4 \sqrt { 5 }$，
$S _ { \triangle A B N } = S _ { \triangle M A D } = \frac { 1 } { 2 } × 2 × 4 = 4$．
$\therefore S _ { \text { 四边形 } B C M N } = S _ { \text { 矩形 } A B C D } - S _ { \triangle A B N } - S _ { \triangle M A D } =$
$4 \sqrt { 5 } - 8$．

19. 如图①,在正方形 $ABCD$ 中,$E$,$F$,$G$,$H$ 分别为 $AB$,$BC$,$CD$,$DA$ 上的点,$HA = EB = FC = GD$,连接 $EG$,$FH$,交点为 $O$.

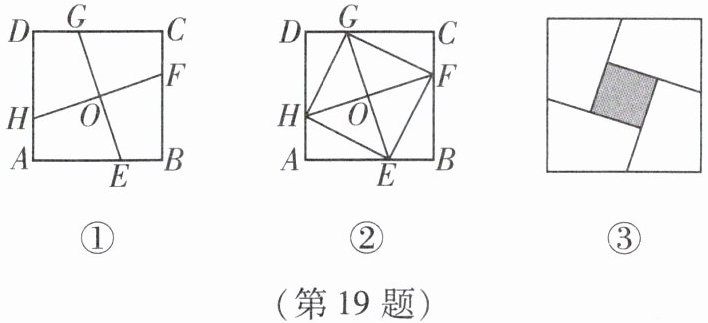
(1) 如图②,连接 $EF$,$FG$,$GH$,$HE$. 试判断四边形 $EFGH$ 的形状,并证明你的结论；
(2) 将正方形 $ABCD$ 沿线段 $EG$,$HF$ 剪开,再把得到的 $4$ 个四边形按图③所示的方式拼接成一个四边形. 若正方形 $ABCD$ 的边长为 $3 cm$,$HA = EB = FC = GD = 1 cm$,则图③中阴影部分的面积为______1$cm^{2}$.

答案：
(1) 四边形 $EFGH$ 是正方形，证明略．
(2) 1