《2025年假日数学吉林出版集团股份有限公司八年级人教版》

17. 问题情境：
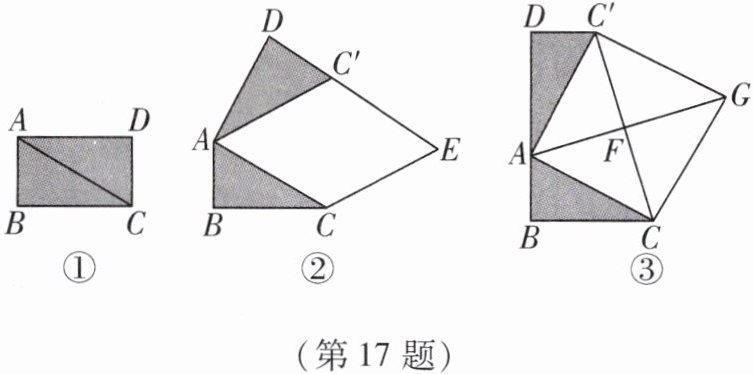
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动,如图①,将矩形纸片$ABCD沿对角线AC$剪开,得到$\triangle ABC和\triangle ACD$,并且量得$AB= 2cm,AC= 4cm$.
操作发现：
(1) 将图①中的$\triangle ACD以点A$为旋转中心,按逆时针方向旋转$∠α$,使$∠α=∠BAC$,得到如图②所示的$\triangle AC'D$,过点$C作AC'$的平行线,与$DC'的延长线交于点E$,则四边形$ACEC'$的形状是菱形；
(2) 创新小组将图①中的$\triangle ACD以点A$为旋转中心,按逆时针方向旋转,使$B$,$A$,$D$三点在同一条直线上,得到如图③所示的$\triangle AC'D$,连接$CC'$,取$CC'的中点F$,连接$AF并延长到点G$,使$FG= AF$,连接$CG$,$C'G$,得到四边形$ACGC'$,发现它是正方形. 请你证明这个结论.

答案：
(1) 菱形
(2) 在图①中，
∵ 四边形 ABCD 是矩形，
∴ $AB // CD$，$AD // BC$。
∴ $\angle CAD = \angle ACB$，$\angle B = 90^{\circ}$。
∴ $\angle BAC + \angle ACB = 90^{\circ}$。
在图③中，由旋转的性质得，
$\angle DAC' = \angle DAC$，
∴ $\angle ACB = \angle DAC'$。
∴ $\angle BAC + \angle DAC' = 90^{\circ}$。
∵ 点 D，A，B 在同一条直线上，
∴ $\angle CAC' = 90^{\circ}$。
由旋转的性质得，$AC = AC'$，
∵ F 是 $CC'$ 的中点，
∴ $AG \perp CC'$，$CF = C'F$。
∵ $AF = FG$，
∴ 四边形 $ACGC'$ 是平行四边形。
∵ $AG \perp CC'$，
∴ $□ ACGC'$ 是菱形。
∵ $\angle CAC' = 90^{\circ}$，
∴ 菱形 $ACGC'$ 是正方形。

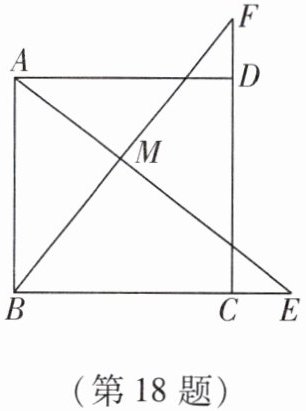
18. 如图,在正方形$ABCD$中,点$E在BC$边的延长线上,点$F在CD$边的延长线上,且$CE= DF$,连接$AE和BF相交于点M$. 求证：$AE= BF$.

证明：证明△AEB≌△BFC

答案： 提示：证明 $\triangle AEB \cong \triangle BFC$。