《2025年假日数学吉林出版集团股份有限公司八年级人教版》

11. 已知a,b,c为△ABC三边的长,且满足$a^{2}c^{2}-b^{2}c^{2}= a^{4}-b^{4}$,试判定△ABC的形状.

答案： 由$a^{2}c^{2}-b^{2}c^{2}=a^{4}-b^{4}$，
得$(a^{2}+b^{2})(a^{2}-b^{2})-c^{2}(a^{2}-b^{2})=0$，
$(a^{2}+b^{2}-c^{2})(a^{2}-b^{2})=0$，
$\therefore a^{2}+b^{2}-c^{2}=0$或$a^{2}-b^{2}=0$，
即$a^{2}+b^{2}=c^{2}$或$a=b$，
或者$a^{2}+b^{2}=c^{2}$且$a=b$．
$\therefore \triangle ABC$为直角三角形或等腰三角形或等腰直角三角形．

12. 如图,在四边形ABCD中,∠A= ∠C= 45°,∠ADB= ∠ABC= 105°.

(1)若AD= 2,求AB的长；$\sqrt {2}+\sqrt {6}$
(2)若AB+CD= 2√3+2,求AB的长.$1+\sqrt {3}$

答案： 1. （1）
解：
在$\triangle ABD$中，$\angle A = 45^{\circ}$，$\angle ADB=105^{\circ}$，根据三角形内角和为$180^{\circ}$，可得$\angle ABD = 180^{\circ}-\angle A-\angle ADB=180^{\circ}-45^{\circ}-105^{\circ}=30^{\circ}$。
由正弦定理$\frac{AD}{\sin\angle ABD}=\frac{AB}{\sin\angle ADB}$。
已知$AD = 2$，$\sin\angle ABD=\sin30^{\circ}=\frac{1}{2}$，$\sin\angle ADB=\sin105^{\circ}=\sin(60^{\circ}+45^{\circ})=\sin60^{\circ}\cos45^{\circ}+\cos60^{\circ}\sin45^{\circ}=\frac{\sqrt{3}}{2}×\frac{\sqrt{2}}{2}+\frac{1}{2}×\frac{\sqrt{2}}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$。
代入正弦定理$\frac{2}{\frac{1}{2}}=\frac{AB}{\frac{\sqrt{6}+\sqrt{2}}{4}}$，则$AB=\sqrt{6}+\sqrt{2}$。
2. （2）
解：
设$AB = x$。
在$\triangle ABD$中，由正弦定理$\frac{AD}{\sin\angle ABD}=\frac{AB}{\sin\angle ADB}$，$\angle ABD = 30^{\circ}$，$\angle ADB = 105^{\circ}$，$\angle A = 45^{\circ}$，可得$AD=\frac{AB\sin\angle ABD}{\sin\angle ADB}=\frac{x\sin30^{\circ}}{\sin105^{\circ}}$。
在$\triangle BCD$中，$\angle C = 45^{\circ}$，$\angle BDC=180^{\circ}-105^{\circ}=75^{\circ}$，$\angle DBC=180^{\circ}-45^{\circ}-75^{\circ}=60^{\circ}$。
由正弦定理$\frac{CD}{\sin\angle DBC}=\frac{BD}{\sin\angle C}$，在$\triangle ABD$中，$\frac{BD}{\sin\angle A}=\frac{AB}{\sin\angle ADB}$，则$BD=\frac{AB\sin\angle A}{\sin\angle ADB}$。
所以$CD=\frac{BD\sin\angle DBC}{\sin\angle C}=\frac{AB\sin\angle A\sin\angle DBC}{\sin\angle ADB\sin\angle C}$。
因为$\sin\angle A=\sin45^{\circ}=\frac{\sqrt{2}}{2}$，$\sin\angle DBC=\sin60^{\circ}=\frac{\sqrt{3}}{2}$，$\sin\angle C=\sin45^{\circ}=\frac{\sqrt{2}}{2}$，$\sin\angle ADB=\sin105^{\circ}=\frac{\sqrt{6}+\sqrt{2}}{4}$。
则$CD=\frac{x×\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}}{\frac{\sqrt{6}+\sqrt{2}}{4}×\frac{\sqrt{2}}{2}}×\frac{\sqrt{2}}{2}=\frac{\sqrt{3}x}{\sqrt{6}+\sqrt{2}}×\frac{\sqrt{2}}{2}=\frac{\sqrt{3}x}{\sqrt{3} + 1}$。
已知$AB + CD=2\sqrt{3}+2$，即$x+\frac{\sqrt{3}x}{\sqrt{3}+1}=2\sqrt{3}+2$。
通分$\frac{(\sqrt{3}+1)x+\sqrt{3}x}{(\sqrt{3}+1)}=2\sqrt{3}+2$，$\frac{(2\sqrt{3}+1)x}{\sqrt{3}+1}=2\sqrt{3}+2$。
$x = 2$。
综上，（1）$AB=\sqrt{6}+\sqrt{2}$；（2）$AB = 2$。

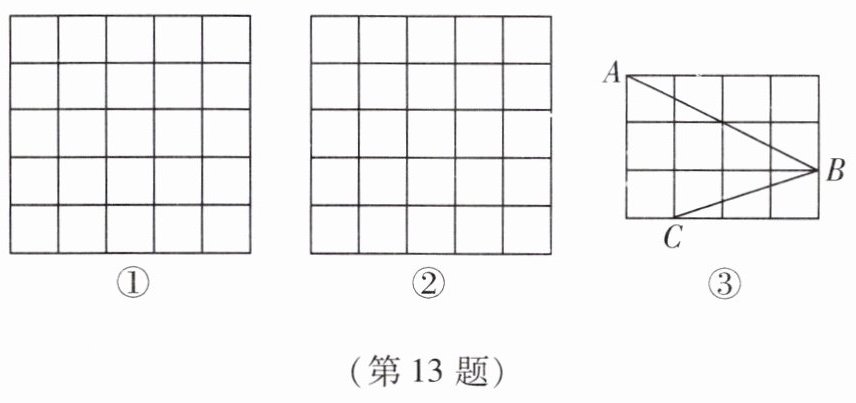
13. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图①中以格点为顶点画一个面积为10的正方形；如图①所示．(答案不唯一)
(2)在图②中以格点为顶点画一个三角形,使三角形三边长分别为2,$\sqrt 5,\sqrt {13}$；如图②所示．(答案不唯一)
(3)如图③,点A,B,C是小正方形的顶点,求∠ABC的度数.45°

答案：

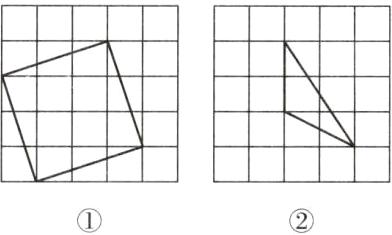
(1)如图①所示．(答案不唯一)
(2)如图②所示．(答案不唯一)
(3)如图③所示，$∠ABC=∠BAC=45^{\circ }$．