《2025年假日数学吉林出版集团股份有限公司八年级人教版》

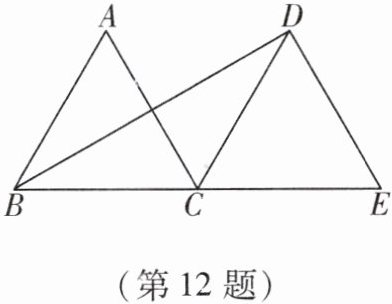
12. 如图,$△ABC和△DCE$都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,求BD的长.$4 \sqrt { 3 }$

答案： $4 \sqrt { 3 }$

13. 如图,在四边形ABCD中,$∠ABC = 90^{\circ}$,$CD⊥AD$,$AD^{2}+CD^{2}= 2AB^{2}$.
(1)求证：$AB = BC$；
连接$AC$，由勾股定理得$AB^{2}+BC^{2}=AC^{2}$，$AD^{2}+CD^{2}=AC^{2}$，结合$AD^{2}+CD^{2}=2AB^{2}$，推出$AB = BC$。
(2)当$BE⊥AD$于点E时,求证：$BE = AE + CD$.
过$C$作$CF\perp BE$于$F$，证四边形$CDEF$是矩形得$CD = EF$，证$\triangle ABE\cong\triangle BCF$得$AE = BF$，由$BE=BF + EF$得$BE = AE + CD$。

答案： 【解析】：
(1) 连接$AC$。
因为$\angle ABC = 90^{\circ}$，根据勾股定理可得$AB^{2}+BC^{2}=AC^{2}$。
又因为$CD\perp AD$，所以$\angle ADC = 90^{\circ}$，根据勾股定理可得$AD^{2}+CD^{2}=AC^{2}$。
已知$AD^{2}+CD^{2}=2AB^{2}$，所以$AC^{2}=2AB^{2}$，即$AB^{2}+BC^{2}=2AB^{2}$，移项可得$BC^{2}=AB^{2}$，所以$AB = BC$。
(2) 过$C$作$CF\perp BE$于$F$。
因为$BE\perp AD$，$CD\perp AD$，$CF\perp BE$，所以四边形$CDEF$是矩形，则$CD = EF$，$\angle CFE=\angle BFC = 90^{\circ}$，$\angle AEB = 90^{\circ}$。
所以$\angle ABE+\angle BAE = 90^{\circ}$，又因为$\angle ABC = 90^{\circ}$，即$\angle ABE+\angle FBC = 90^{\circ}$，所以$\angle BAE=\angle FBC$。
在$\triangle ABE$和$\triangle BCF$中，$\left\{\begin{array}{l}\angle AEB=\angle BFC\\\angle BAE=\angle FBC\\AB = BC\end{array}\right.$，根据$AAS$（角角边）定理可得$\triangle ABE\cong\triangle BCF$。
所以$AE = BF$。
因为$BE=BF + EF$，$AE = BF$，$CD = EF$，所以$BE = AE + CD$。
【答案】：
(1) 连接$AC$，由勾股定理得$AB^{2}+BC^{2}=AC^{2}$，$AD^{2}+CD^{2}=AC^{2}$，结合$AD^{2}+CD^{2}=2AB^{2}$，推出$AB = BC$。
(2) 过$C$作$CF\perp BE$于$F$，证四边形$CDEF$是矩形得$CD = EF$，证$\triangle ABE\cong\triangle BCF$得$AE = BF$，由$BE=BF + EF$得$BE = AE + CD$。

14. 如图,在$4×4$的正方形网格中,每个小方格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图①中,画一个直角三角形,使它的三边长都是有理数；图①中，如直角边为$3$和$4$，斜边为$5$的直角三角形（画法不唯一）
(2)在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数；图②中，如直角边为$2$，另一直角边为$\sqrt{2}$，斜边为$\sqrt{6}$的直角三角形（画法不唯一）
(3)在图③中,画一个直角三角形,使它的三边长都是无理数.图③中，如三边为$\sqrt{2}$，$\sqrt{8}$，$\sqrt{10}$的直角三角形（画法不唯一）

答案： 【解析】：
(1) 利用勾股定理的逆定理，找三边满足$a^{2}+b^{2}=c^{2}$且$a,b,c$为有理数的情况。例如$3,4,5$，在图①中，横向取$3$个格，纵向取$4$个格，连接端点与起点构成直角三角形（答案不唯一）。
(2) 设直角三角形三边为$a,b,c$（$c$为斜边），取$a = 2$（有理数），根据勾股定理构造$b=\sqrt{2}$，$c=\sqrt{6}$（$2^{2}+(\sqrt{2})^{2}=(\sqrt{6})^{2}$不成立，重新构造：取直角边为$2$（有理数），另一直角边为$\sqrt{2}$（由边长为$1$的正方形对角线得到），斜边$\sqrt{2^{2}+(\sqrt{2})^{2}}=\sqrt{4 + 2}=\sqrt{6}$。在图②中按此构造（答案不唯一）。
(3) 利用正方形对角线（长度为$\sqrt{2}$，无理数），取三边为$\sqrt{2},\sqrt{8},\sqrt{10}$（$(\sqrt{2})^{2}+(\sqrt{8})^{2}=2 + 8 = 10=(\sqrt{10})^{2}$）。在图③中，通过连接格点得到边长为$\sqrt{2}$（小正方形对角线）、$\sqrt{8}=2\sqrt{2}$（两个小正方形对角线组成）、$\sqrt{10}$（横向$1$个格，纵向$3$个格的两点距离$\sqrt{1^{2}+3^{2}}=\sqrt{10}$）的直角三角形（答案不唯一）。
【答案】：
(1) 图①中，如直角边为$3$和$4$，斜边为$5$的直角三角形（画法不唯一）。
(2) 图②中，如直角边为$2$，另一直角边为$\sqrt{2}$，斜边为$\sqrt{6}$的直角三角形（画法不唯一）。
(3) 图③中，如三边为$\sqrt{2}$，$\sqrt{8}$，$\sqrt{10}$的直角三角形（画法不唯一）。