第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
5. 如图,在平面直角坐标系中,Rt△OAB的斜边OA在第一象限,并与x轴的正半轴夹角为30°.C为OA的中点,BC= 1,则点A的坐标为(
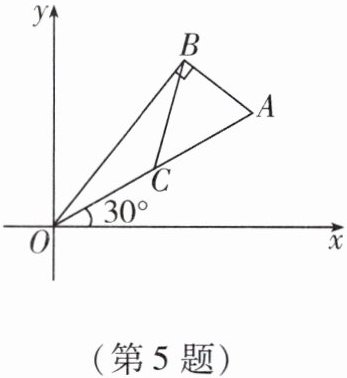
A.$(\sqrt {3},\sqrt {3})$
B.$(\sqrt {3},1)$
C.(2,1)
D.$(2,\sqrt {3})$
B
)
A.$(\sqrt {3},\sqrt {3})$
B.$(\sqrt {3},1)$
C.(2,1)
D.$(2,\sqrt {3})$
答案:
B
6. 若一个三角形的三边长分别为3,4,x,要使此三角形是直角三角形,则x的值是
5 或$\sqrt {7}$
.
答案:
5 或$\sqrt {7}$
7. 如图①,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图②所示放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图②中阴影部分的面积为
$4\sqrt {5}$
.
答案:
$4\sqrt {5}$
8. 若等腰三角形两边长分别为4和6,则底边上的高为
$4\sqrt {2}$或$\sqrt {7}$
.
答案:
$4\sqrt {2}$或$\sqrt {7}$
9. 为了比较$\sqrt {5}+1与\sqrt {10}$的大小,可以构造如图所示的图形进行推算,其中∠C= 90°,BC= 3,点D在BC上,且BD= AC= 1.通过计算可得$\sqrt {5}+1$
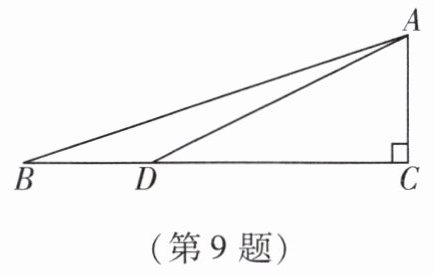
>
$\sqrt {10}$.(选填“>”“<”或“=”)
答案:
>
10. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时捕捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC= 90°,点M,N分别在射线BA,BC上,MN长度始终保持不变,MN= 4,E为MN的中点,点D到BA,BC的距离分别为4和2.在此滑动过程中,猫与老鼠的距离DE的最小值为______
2√5 - 2
.
答案:
$2\sqrt {5}-2$
查看更多完整答案,请扫码查看


