第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
15. 有这样一类题目:化简 $\sqrt {a\pm 2\sqrt {b}}$. 如果你能找到两个数 $m$,$n$,使 $m^{2}+n^{2}= a$,并且 $mn= \sqrt {b}$,那么将 $a\pm 2\sqrt {b}$ 变成 $m^{2}+n^{2}\pm 2mn= (m\pm n)^{2}$,再开方使 $\sqrt {a\pm 2\sqrt {b}}$ 化简.
例如:化简 $\sqrt {3\pm 2\sqrt {2}}$.
因为 $\sqrt {3\pm 2\sqrt {2}}= \sqrt {1+2\pm 2\sqrt {2}}= \sqrt {1^{2}+(\sqrt {2})^{2}\pm 2\sqrt {2}}= \sqrt {(1\pm \sqrt {2})^{2}}$,
所以 $\sqrt {3\pm 2\sqrt {2}}= \sqrt {(1\pm \sqrt {2})^{2}}= \sqrt {2}\pm 1$.
仿照上例化简下列各式:
(1) $\sqrt {9+4\sqrt {5}}$=
(2) $\sqrt {18-2\sqrt {77}}$=
例如:化简 $\sqrt {3\pm 2\sqrt {2}}$.
因为 $\sqrt {3\pm 2\sqrt {2}}= \sqrt {1+2\pm 2\sqrt {2}}= \sqrt {1^{2}+(\sqrt {2})^{2}\pm 2\sqrt {2}}= \sqrt {(1\pm \sqrt {2})^{2}}$,
所以 $\sqrt {3\pm 2\sqrt {2}}= \sqrt {(1\pm \sqrt {2})^{2}}= \sqrt {2}\pm 1$.
仿照上例化简下列各式:
(1) $\sqrt {9+4\sqrt {5}}$=
$2 + \sqrt{5}$
;(2) $\sqrt {18-2\sqrt {77}}$=
$\sqrt{11} - \sqrt{7}$
.
答案:
(1) $ \sqrt{9 + 4 \sqrt{5}} $
$ = \sqrt{4 + 5 + 4 \sqrt{5}} $
$ = \sqrt{2^{2} + (\sqrt{5})^{2} + 4 \sqrt{5}} $
$ = \sqrt{(2 + \sqrt{5})^{2}} $
$ = 2 + \sqrt{5} $
(2) $ \sqrt{18 - 2 \sqrt{77}} $
$ = \sqrt{11 + 7 - 2 \sqrt{77}} $
$ = \sqrt{(\sqrt{11})^{2} + (\sqrt{7})^{2} - 2 \sqrt{77}} $
$ = \sqrt{(\sqrt{11} - \sqrt{7})^{2}} $
$ = \sqrt{11} - \sqrt{7} $
(1) $ \sqrt{9 + 4 \sqrt{5}} $
$ = \sqrt{4 + 5 + 4 \sqrt{5}} $
$ = \sqrt{2^{2} + (\sqrt{5})^{2} + 4 \sqrt{5}} $
$ = \sqrt{(2 + \sqrt{5})^{2}} $
$ = 2 + \sqrt{5} $
(2) $ \sqrt{18 - 2 \sqrt{77}} $
$ = \sqrt{11 + 7 - 2 \sqrt{77}} $
$ = \sqrt{(\sqrt{11})^{2} + (\sqrt{7})^{2} - 2 \sqrt{77}} $
$ = \sqrt{(\sqrt{11} - \sqrt{7})^{2}} $
$ = \sqrt{11} - \sqrt{7} $
16. 图①、图②都是 $4×4$ 的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为 1. 在每个网格中标注了 5 个格点,按下列要求画图:
(1) 在图①中以格点为顶点画一个等腰三角形,使其内部已标注的格点只有 3 个;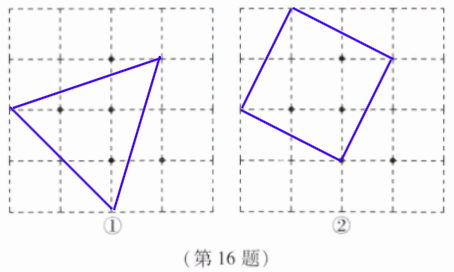
(2) 在图②中,以格点为顶点,画一个正方形,使其内部已标注的格点只有 3 个,且边长为无理数.
(1) 在图①中以格点为顶点画一个等腰三角形,使其内部已标注的格点只有 3 个;

(2) 在图②中,以格点为顶点,画一个正方形,使其内部已标注的格点只有 3 个,且边长为无理数.

答案:


查看更多完整答案,请扫码查看


