2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1.如图,一只蚂蚁从长、宽都是3cm,高是8cm的长方体纸盒的A点沿纸盒爬到B点,那么它所爬行的最短路线的长是()
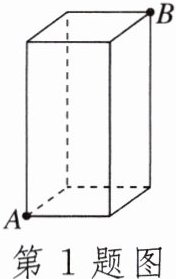
A.$(3\sqrt {2}+8)cm$
B.10cm
C.$\sqrt {130}cm$
D.14cm

A.$(3\sqrt {2}+8)cm$
B.10cm
C.$\sqrt {130}cm$
D.14cm
答案:
B
2.如图,在$Rt△ABC$中,$∠ACB= 90^{\circ },AC= 6,$$BC= 8$,AD是$∠BAC$的平分线.若P,Q分别是AD和AC上的动点,则$PC+PQ$的最小值是()
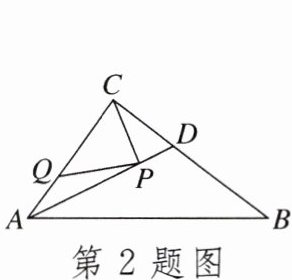
A.$\frac {12}{5}$
B.4
C.$\frac {24}{5}$
D.5

A.$\frac {12}{5}$
B.4
C.$\frac {24}{5}$
D.5
答案:
C 解析:如图,过点C作CM⊥AB交AB于点M,交AD于点P,过点P作PQ⊥AC于点Q.
∵AD是∠BAC的平分线,
∴PQ=PM.这时PC+PQ有最小值,即CM的长度.
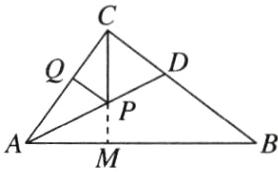
∵AC=6,BC=8,∠ACB=90°,
∴AB= $\sqrt{AC²+BC²}$ = $\sqrt{6²+8²}$ =10.
∵S_{△ABC}=$\frac{1}{2}$AB·CM=$\frac{1}{2}$AC·BC,
∴CM=$\frac{AC·BC}{AB}$=$\frac{6×8}{10}$=$\frac{24}{5}$,即PC+PQ的最小值为$\frac{24}{5}$.故选C.
C 解析:如图,过点C作CM⊥AB交AB于点M,交AD于点P,过点P作PQ⊥AC于点Q.
∵AD是∠BAC的平分线,
∴PQ=PM.这时PC+PQ有最小值,即CM的长度.

∵AC=6,BC=8,∠ACB=90°,
∴AB= $\sqrt{AC²+BC²}$ = $\sqrt{6²+8²}$ =10.
∵S_{△ABC}=$\frac{1}{2}$AB·CM=$\frac{1}{2}$AC·BC,
∴CM=$\frac{AC·BC}{AB}$=$\frac{6×8}{10}$=$\frac{24}{5}$,即PC+PQ的最小值为$\frac{24}{5}$.故选C.
3.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是____尺.
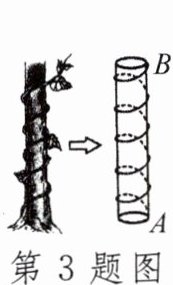

答案:
25
4.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器右侧内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器左侧外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路程是____.
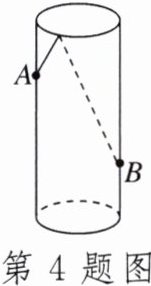

答案:
13cm 解析:如图,作A关于EF的对称点A',连接A'B,则A'B即为最短路程,A'B=$\sqrt{A'D²+BD²}$=$\sqrt{5²+12²}$=13(cm).

13cm 解析:如图,作A关于EF的对称点A',连接A'B,则A'B即为最短路程,A'B=$\sqrt{A'D²+BD²}$=$\sqrt{5²+12²}$=13(cm).

5.如图是一个三级台阶,它的每一级的长、宽和高分别等于5dm,3dm和1dm,A和B是这个台阶的两个相对的端点,A点上有一只春蚕,想到B点去吃可口的桑叶.这只春蚕从A点出发,沿着台阶面爬到B点,请你求出它爬行的最短路程.
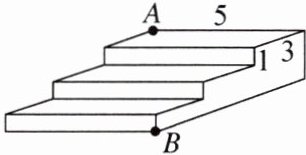

答案:
解:如图,将台阶面展开.在Rt△ACB中,AC=3×3+1×3=12(dm),BC=5dm,由勾股定理得AB²=AC²+BC²,所以AB=13dm.故春蚕爬行的最短路程为13dm.

解:如图,将台阶面展开.在Rt△ACB中,AC=3×3+1×3=12(dm),BC=5dm,由勾股定理得AB²=AC²+BC²,所以AB=13dm.故春蚕爬行的最短路程为13dm.

查看更多完整答案,请扫码查看


