《2025年时习之暑假衔接八年级数学湘教版》

1. 在中国有很多吉祥的图案深受大家喜爱,人们会用这些图案来装饰生活,祈求平安.比如下列图案分别表示“福”“禄”“寿”“喜”,其中既是轴对称图形,又是中心对称图形的有()

A. 1个 B. 2个 C. 3个 D. 4个

答案： B

2. 如图,△ABC与$△A_1B_1C_1$关于点O成中心对称,下列说法：$①∠BAC= ∠B_1A_1C_1；$$②AC= A_1C_1；$$③OA= OA_1；$④△ABC与$△A_1B_1C_1$的面积相等.其中正确的有()

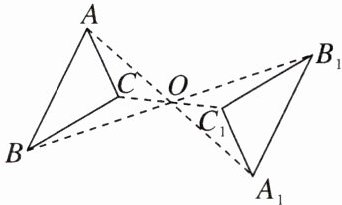
A.1个

B.2个

C.3个

D.4个

答案： D

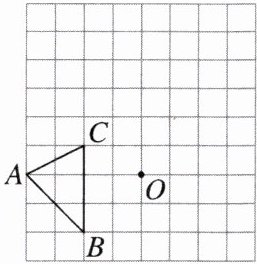
3. 如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A,B,C及点O均在格点上,请按要求完成以下操作：
(1)将△ABC向上平移4个单位,得到$△A_1B_1C_1($不写作法,但要标出字母)；
(2)作出△ABC关于点O的中心对称图形$△A_2B_2C_2($不写作法,但要标出字母).

答案：
解:
(1)△A₁B₁C₁如图所示.
(2)△A₂B₂C₂如图所示.
　　　　　　　　

4. 如图,为了测量一个池塘两端A,B间的距离,小聪先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为10m,则A,B间的距离为()

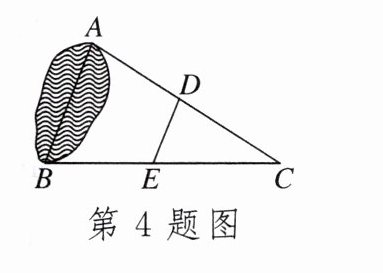
A. 15m
B. 25m
C. 30m
D. 20m

答案： D

5. 如图,在▱ABCD中,P是BC边上的一个动点,M,N分别是PA,PD的中点,在点P的运动过程中,MN的长度()

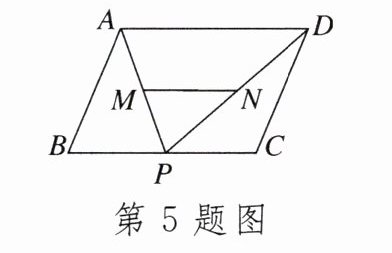
A. 先变大再变小
B. 先变小再变大
C. 不变
D. 不能确定

答案： C

6. 如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD= 30厘米,△OAB的周长是20厘米,则EF= ______厘米.

答案： 2.5　解析:
∵四边形ABCD为平行四边形，
∴OA+OB=$\frac {1}{2}$(AC+BD)=15厘米.
∵△OAB的周长为20厘米，
∴AB+OA+OB=20厘米.
∴AB=5厘米.又
∵E,F为OA,OB的中点，
∴EF=$\frac {1}{2}$AB=2.5厘米.

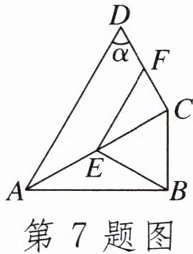
7. 如图,在四边形ABCD中,AC平分∠BAD,∠ACD= ∠ABC= 90°,E,F分别为AC,CD的中点,∠D= α,则∠BEF的度数为______(用含α的式子表示).

答案： 270°−3α　解析:
∵∠ACD=90°,∠D=α,
∴∠DAC=90°−α.
∵AC平分∠BAD，
∴∠DAC=∠BAC=90°−α.
∵∠ABC=90°,E为AC的中点，
∴BE=AE=EC.
∴∠EAB=∠EBA=90°−α.
∴∠CEB=180°−2α.
∵E,F分别为AC,CD的中点，
∴EF//AD.
∴∠CEF=∠DAC=90°−α.
∴∠BEF=∠CEB+∠CEF=180°−2α+90°−α=270°−3α.故答案为270°−3α.