2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1.如图是某公园内的正六边形座椅,则$∠ABC$的度数为____.


答案:
$120^{\circ}$
2.已知在▱ABCD中,$∠A+∠C= 80^{\circ}$,则$∠B$的度数是____.
答案:
$140^{\circ}$
3.某科技小组制作了一个机器人,它能根据指令要求进行行走和旋转,某一指令规定:机器人先向前行走1m,然后左转$36^{\circ}$.若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了____m.
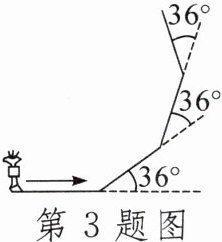

答案:
10
4.如图,在▱ABCD中,$∠ABC= 60^{\circ}$,E,F分别在CD和BC的延长线上,$AE// BD$,$EF⊥BC$,$EF= \sqrt{3}$,则AB的长是____.
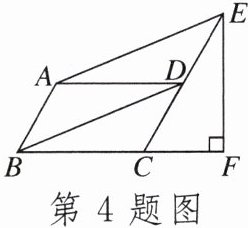

答案:
1 解析:
∵四边形ABCD为平行四边形,$\therefore AB// CE$,$AB=CD$.$\because AE// BD$,$\therefore$四边形ABDE为平行四边形.$\therefore AB=DE=DC$.$\because AB// CD$,$\therefore ∠ECF=∠ABC=60^{\circ}$.$\because EF⊥BC$,$\therefore ∠F=90^{\circ}$.$\therefore ∠CEF=30^{\circ}$.设$CE=x$,则$CF=\frac{1}{2}x$,$\therefore \sqrt{x^{2}-(\frac{1}{2}x)^{2}}=\sqrt{3}$,$\therefore x=2$.$\therefore AB=\frac{1}{2}×2=1$.
∵四边形ABCD为平行四边形,$\therefore AB// CE$,$AB=CD$.$\because AE// BD$,$\therefore$四边形ABDE为平行四边形.$\therefore AB=DE=DC$.$\because AB// CD$,$\therefore ∠ECF=∠ABC=60^{\circ}$.$\because EF⊥BC$,$\therefore ∠F=90^{\circ}$.$\therefore ∠CEF=30^{\circ}$.设$CE=x$,则$CF=\frac{1}{2}x$,$\therefore \sqrt{x^{2}-(\frac{1}{2}x)^{2}}=\sqrt{3}$,$\therefore x=2$.$\therefore AB=\frac{1}{2}×2=1$.
5.如图,▱ABCD的周长为20cm,AE平分$∠BAD$.若$CE= 2cm$,则AB的长是()
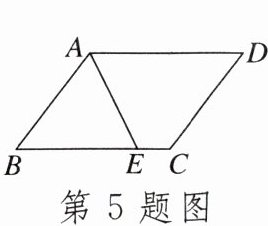
A.10cm
B.8cm
C.6cm
D.4cm

A.10cm
B.8cm
C.6cm
D.4cm
答案:
D 解析:
∵四边形ABCD是平行四边形,$\therefore AD// BC$.$\therefore ∠BEA=∠EAD$.$\because AE$平分$∠BAD$,$\therefore ∠BAE=∠EAD$.$\therefore ∠BAE=∠BEA$.$\therefore AB=BE$.设$AB=xcm$,则$BC=(x+2)cm$.则$2(x+x+2)=20$,解得$x=4$.故选D.
∵四边形ABCD是平行四边形,$\therefore AD// BC$.$\therefore ∠BEA=∠EAD$.$\because AE$平分$∠BAD$,$\therefore ∠BAE=∠EAD$.$\therefore ∠BAE=∠BEA$.$\therefore AB=BE$.设$AB=xcm$,则$BC=(x+2)cm$.则$2(x+x+2)=20$,解得$x=4$.故选D.
6.如图,在▱ABCD中,对角线AC与BD相交于点O,过点O任作一条直线分别交AB,CD于点E,F.
(1)求证:$OE= OF$;
(2)若$AB= 7$,$BC= 5$,$OE= 2$,求四边形BCFE的周长.
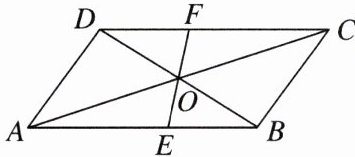
(1)求证:$OE= OF$;
(2)若$AB= 7$,$BC= 5$,$OE= 2$,求四边形BCFE的周长.

答案:
(1)证明:
∵四边形ABCD为平行四边形,$\therefore OA=OC$,$DC// AB$.$\therefore ∠BAO=∠DCO$.在$△AOE$和$△COF$中,$\begin{cases} ∠EAO=∠FCO,\\ OA=OC,\\ ∠EOA=∠FOC, \end{cases}$$\therefore △AOE\cong △COF(ASA)$.$\therefore OE=OF$.
(2)解:由
(1)可得$OF=OE=2$,$AE=CF$,$\therefore EF=4$.$\therefore$四边形BCFE的周长为$BE+BC+CF+EF=(BE+CF)+BC+EF=AB+BC+EF=7+5+4=16$.
(1)证明:
∵四边形ABCD为平行四边形,$\therefore OA=OC$,$DC// AB$.$\therefore ∠BAO=∠DCO$.在$△AOE$和$△COF$中,$\begin{cases} ∠EAO=∠FCO,\\ OA=OC,\\ ∠EOA=∠FOC, \end{cases}$$\therefore △AOE\cong △COF(ASA)$.$\therefore OE=OF$.
(2)解:由
(1)可得$OF=OE=2$,$AE=CF$,$\therefore EF=4$.$\therefore$四边形BCFE的周长为$BE+BC+CF+EF=(BE+CF)+BC+EF=AB+BC+EF=7+5+4=16$.
小明不小心打破了一块平行四边形玻璃,如图所示为其中一块.现需要购买一块相同的玻璃,满足相邻两边AB,BC的长分别为30cm,50cm,且$∠ABC= 60^{\circ}$.根据所学知识选择多种方法画出顶点D的位置,并说明理由.
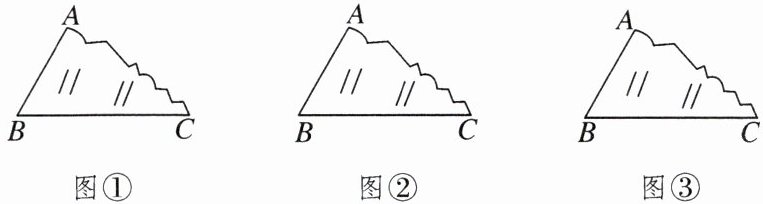

答案:
解:如图①,以点A为圆心,线段BC的长为半径画弧,再以点C为圆心,线段AB的长为半径画弧,两弧相交于点D,则$AD=BC$,$AB=CD$,$\therefore$四边形ABCD为平行四边形,则点D即为所求.如图②,连接AC,先作线段AC的垂直平分线,交AC于点O,再作射线BO,以点O为圆心,BO的长为半径画弧,交射线BO于点D,此时$AO=OC$,$OB=OD$,$\therefore$四边形ABCD为平行四边形,则点D即为所求.如图③,延长BA至点M,延长BC于点N,根据作一个角等于已知角的方法作$∠MAD=∠ABC$,$∠NCD=∠ABC$,$AD$与$CD$交于点D,则$AD// BC$,$AB// CD$,$\therefore$四边形ABCD为平行四边形,则点D即为所求.如图④,延长BA至点M,根据作一个角等于已知角的方法作$∠MAN=∠ABC$,再以点A为圆心,线段BC的长为半径画弧,交射线AN于点D,此时$AD// BC$,且$AD=BC$,$\therefore$四边形ABCD为平行四边形,则点D即为所求.如图⑤,过点A作BC的垂线,交BC于点E,再以点C为圆心,线段BE的长为半径画弧,交BC的延长线于点F,最后过点F作直线CF的垂线,以点F为圆心,线段AE的长为半径画弧,交直线CF的垂线于点D,此时$△ABE\cong △DCF(SAS)$,$\therefore AB=CD$,$∠ABC=∠DCF$.$\therefore AB// CD$.$\therefore$四边形ABCD为平行四边形,则点D即为所求.(任选3种即可)



解:如图①,以点A为圆心,线段BC的长为半径画弧,再以点C为圆心,线段AB的长为半径画弧,两弧相交于点D,则$AD=BC$,$AB=CD$,$\therefore$四边形ABCD为平行四边形,则点D即为所求.如图②,连接AC,先作线段AC的垂直平分线,交AC于点O,再作射线BO,以点O为圆心,BO的长为半径画弧,交射线BO于点D,此时$AO=OC$,$OB=OD$,$\therefore$四边形ABCD为平行四边形,则点D即为所求.如图③,延长BA至点M,延长BC于点N,根据作一个角等于已知角的方法作$∠MAD=∠ABC$,$∠NCD=∠ABC$,$AD$与$CD$交于点D,则$AD// BC$,$AB// CD$,$\therefore$四边形ABCD为平行四边形,则点D即为所求.如图④,延长BA至点M,根据作一个角等于已知角的方法作$∠MAN=∠ABC$,再以点A为圆心,线段BC的长为半径画弧,交射线AN于点D,此时$AD// BC$,且$AD=BC$,$\therefore$四边形ABCD为平行四边形,则点D即为所求.如图⑤,过点A作BC的垂线,交BC于点E,再以点C为圆心,线段BE的长为半径画弧,交BC的延长线于点F,最后过点F作直线CF的垂线,以点F为圆心,线段AE的长为半径画弧,交直线CF的垂线于点D,此时$△ABE\cong △DCF(SAS)$,$\therefore AB=CD$,$∠ABC=∠DCF$.$\therefore AB// CD$.$\therefore$四边形ABCD为平行四边形,则点D即为所求.(任选3种即可)



查看更多完整答案,请扫码查看


