2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
6. 在学校组织的研学活动中,辰星小组合作搭建帐篷。如图是他们搭建帐篷的支架示意图。在$\triangle ABC$中,两根支架从帐篷顶点$A$支撑在水平的支架上,一根支架$AD\perp BC于点D$,另一根支架$AE的端点E在线段BD$上,且$AE= BE$。经测量,知$BD= 1.6m$,$AD= 1.2m$,$AC= 1.5m$。根据测量结果,解答下列问题:
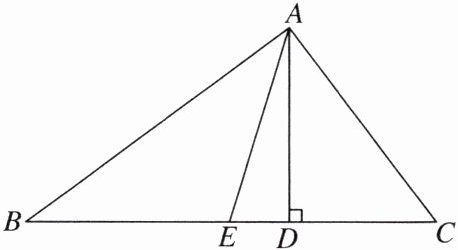
(1)求$AE$的长。
(2)按照要求,当帐篷支架$AB与AC$所夹的角度为直角时,帐篷最为稳定。请通过计算说明辰星小组搭建的帐篷是否符合要求。

(1)求$AE$的长。
(2)按照要求,当帐篷支架$AB与AC$所夹的角度为直角时,帐篷最为稳定。请通过计算说明辰星小组搭建的帐篷是否符合要求。
答案:
解:
(1)设$AE=x m$,则$BE=AE=x m$,$ED=(1.6−x) m$。$\because AD \perp BC$,$\therefore \angle ADB = \angle ADC = 90^{ \circ }$。
在$Rt\triangle ADE$中,$AD^{2}+ED^{2}=AE^{2}$,即$1.2^{2}+(1.6−x)^{2}=x^{2}$,解得$x=1.25$。$\therefore AE$的长为$1.25m$。
(2)帐篷符合要求。理由如下:在$Rt\triangle ABD$中,BD = 1.6m,AD = 1.2m,$\therefore AB=\sqrt{1.6^{2}+1.2^{2}}=2(m)$。
在$Rt\triangle ADC$中,$AD = 1.2m$,$AC = 1.5m$,
$\therefore CD=\sqrt{1.5^{2}-1.2^{2}}=0.9(m)$。
$\therefore BC = BD + CD = 2.5(m)$。
$\because AB^{2}+AC^{2}=2^{2}+1.5^{2}=6.25$,$BC^{2}=2.5^{2}=6.25$,
$\therefore AB^{2}+AC^{2}=BC^{2}$。
$\therefore \triangle ABC$是直角三角形,$\angle BAC = 90^{ \circ }$。
$\therefore$帐篷符合要求。
(1)设$AE=x m$,则$BE=AE=x m$,$ED=(1.6−x) m$。$\because AD \perp BC$,$\therefore \angle ADB = \angle ADC = 90^{ \circ }$。
在$Rt\triangle ADE$中,$AD^{2}+ED^{2}=AE^{2}$,即$1.2^{2}+(1.6−x)^{2}=x^{2}$,解得$x=1.25$。$\therefore AE$的长为$1.25m$。
(2)帐篷符合要求。理由如下:在$Rt\triangle ABD$中,BD = 1.6m,AD = 1.2m,$\therefore AB=\sqrt{1.6^{2}+1.2^{2}}=2(m)$。
在$Rt\triangle ADC$中,$AD = 1.2m$,$AC = 1.5m$,
$\therefore CD=\sqrt{1.5^{2}-1.2^{2}}=0.9(m)$。
$\therefore BC = BD + CD = 2.5(m)$。
$\because AB^{2}+AC^{2}=2^{2}+1.5^{2}=6.25$,$BC^{2}=2.5^{2}=6.25$,
$\therefore AB^{2}+AC^{2}=BC^{2}$。
$\therefore \triangle ABC$是直角三角形,$\angle BAC = 90^{ \circ }$。
$\therefore$帐篷符合要求。
小明同学在延时课上进行了项目式学习实践探究,并绘制了如下记录表格:
|课题|在放风筝时测量风筝离地面的垂直高度$AD$|
|----|----|
|模型抽象||
|测绘数据|

①测得水平距离$ED$的长为15米②根据手中剩余线的长度,计算出风筝线$AB$的长为17米③牵线放风筝的手到地面的距离$BE$为1.6米|
|说明|点$A$,$B$,$E$,$D$在同一平面内|
请根据表格信息,解答下列问题。
(1)求线段$AD$的长;
(2)若想要风筝沿$DA$方向再上升12米,则在$ED$长度不变的前提下,小明同学应该再放出多少米线?
|课题|在放风筝时测量风筝离地面的垂直高度$AD$|
|----|----|
|模型抽象||
|测绘数据|

①测得水平距离$ED$的长为15米②根据手中剩余线的长度,计算出风筝线$AB$的长为17米③牵线放风筝的手到地面的距离$BE$为1.6米|
|说明|点$A$,$B$,$E$,$D$在同一平面内|
请根据表格信息,解答下列问题。
(1)求线段$AD$的长;
(2)若想要风筝沿$DA$方向再上升12米,则在$ED$长度不变的前提下,小明同学应该再放出多少米线?
答案:
解:
(1)如图,过点$B$作$BC \perp AD$于点$C$,在$Rt\triangle ABC$中,$\angle ACB = 90^{ \circ }$,$BC = 15$米,$AB = 17$米,由勾股定理,得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{17^{2}-15^{2}}=8$(米),则$AD = AC + CD = 8 + 1.6 = 9.6$(米)。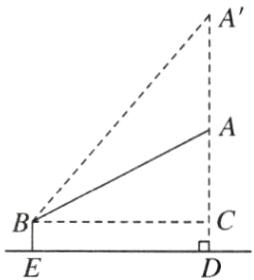
@@解:
(2)如图,设风筝沿$DA$方向再上升$12$米后,到达$A'$处,连接$A'B$,则$A'C = 20$米。$\therefore$此时风筝线的长为$A'B=\sqrt{A'C^{2}+BC^{2}}=25$米。$\therefore 25 - 17 = 8$(米)。答:小明同学应该再放出$8$米线。
解:
(1)如图,过点$B$作$BC \perp AD$于点$C$,在$Rt\triangle ABC$中,$\angle ACB = 90^{ \circ }$,$BC = 15$米,$AB = 17$米,由勾股定理,得$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{17^{2}-15^{2}}=8$(米),则$AD = AC + CD = 8 + 1.6 = 9.6$(米)。

@@解:
(2)如图,设风筝沿$DA$方向再上升$12$米后,到达$A'$处,连接$A'B$,则$A'C = 20$米。$\therefore$此时风筝线的长为$A'B=\sqrt{A'C^{2}+BC^{2}}=25$米。$\therefore 25 - 17 = 8$(米)。答:小明同学应该再放出$8$米线。
查看更多完整答案,请扫码查看


