2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
7.某校科技节上,同学们在操场进行无人机表演,其中甲、乙两架无人机离操场地面的高度y(单位:米)与表演时间x(单位:秒)的图象如图所示.已知表演开始时甲、乙离地的高度分别是5米、15米,在1分钟的表演过程中甲、乙两架无人机的高度差不超过5米的时间可持续______秒.
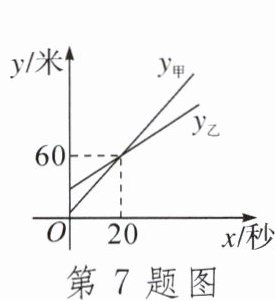

答案:
20
8.某医院研究所开发了一种新药,在实验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)的变化情况如图所示,如果每毫升血液中的含药量为3微克或3微克以上时,治疗疾病最有效,那么这个最有效的时间共有______小时.
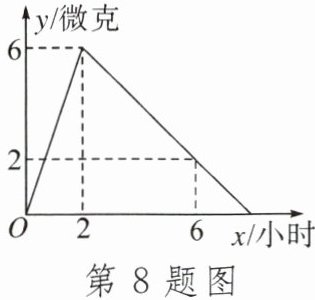

答案:
4
9.某生物小组观察一植物生长,得到植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD//x轴).
(1)该植物从观察时起,多少天以后停止长高?
(2)求线段AC的解析式,并求该植物最高长到多少厘米.
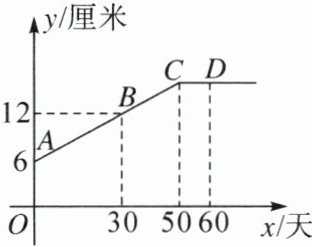
(1)该植物从观察时起,多少天以后停止长高?
(2)求线段AC的解析式,并求该植物最高长到多少厘米.

答案:
解:
(1)$\because CD \parallel x$轴,$\therefore$从第 50 天开始植物的高度不变,即 50 天以后停止长高.
(2)设线段 AC 所在的直线的解析式为$y = kx + b(k \neq 0)$,
$\because$经过点$A(0, 6)$,$B(30, 12)$,
$\therefore \begin{cases}30k + b = 12 \\ b = 6\end{cases}$,
解得$\begin{cases}k = \frac{1}{5} \\ b = 6\end{cases}$,
$\therefore$线段 AC 的解析式为$y = \frac{1}{5}x + 6(0 \leq x \leq 50)$.
当$x = 50$时,$y = \frac{1}{5} \times 50 + 6 = 16$.
即第 50 天,该植物最高长到 16 厘米.
(1)$\because CD \parallel x$轴,$\therefore$从第 50 天开始植物的高度不变,即 50 天以后停止长高.
(2)设线段 AC 所在的直线的解析式为$y = kx + b(k \neq 0)$,
$\because$经过点$A(0, 6)$,$B(30, 12)$,
$\therefore \begin{cases}30k + b = 12 \\ b = 6\end{cases}$,
解得$\begin{cases}k = \frac{1}{5} \\ b = 6\end{cases}$,
$\therefore$线段 AC 的解析式为$y = \frac{1}{5}x + 6(0 \leq x \leq 50)$.
当$x = 50$时,$y = \frac{1}{5} \times 50 + 6 = 16$.
即第 50 天,该植物最高长到 16 厘米.
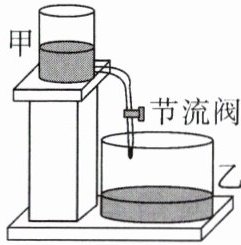
“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组用甲、乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作了如图所示的简易计时装置.他们设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后每隔10min观察一次甲容器中的水面高度,获得的数据如表,发现水面高度h(cm)与流水时间t(min)(t为正整数)之间满足一次函数关系.
|流水时间t/min|0|10|20|30|40|…|
|----|----|----|----|----|----|----|
|水面高度h/cm(观察值)|30|28|26|24|22|…|
(1)求水面高度h与流水时间t之间的函数关系式.
(2)按此速度,流水时间为1h时,水面高度为多少厘米?
(3)按此速度,经过多长时间,甲容器内的水恰好流完?
|流水时间t/min|0|10|20|30|40|…|
|----|----|----|----|----|----|----|
|水面高度h/cm(观察值)|30|28|26|24|22|…|
(1)求水面高度h与流水时间t之间的函数关系式.
(2)按此速度,流水时间为1h时,水面高度为多少厘米?
(3)按此速度,经过多长时间,甲容器内的水恰好流完?

答案:
解:
(1)设水面高度 h 与流水时间 t 之间的函数关系式为$h = kt + b$,
把$(0, 30)$,$(10, 28)$代入得$\begin{cases}b = 30 \\ 10k + b = 28\end{cases}$,
解得$\begin{cases}k = -\frac{1}{5} \\ b = 30\end{cases}$,
$\therefore$水面高度 h 与流水时间 t 之间的函数关系式为$h = -\frac{1}{5}t + 30$.
(2)当$t = 60$时,$h = -\frac{1}{5} \times 60 + 30 = 18$,
$\therefore$流水时间为 1 h 时,水面高度为 18 cm.
(3)当$h = 0$时,$0 = -\frac{1}{5}t + 30$,$\therefore t = 150$,即经过 150 min,甲容器内的水恰好流完.
(1)设水面高度 h 与流水时间 t 之间的函数关系式为$h = kt + b$,
把$(0, 30)$,$(10, 28)$代入得$\begin{cases}b = 30 \\ 10k + b = 28\end{cases}$,
解得$\begin{cases}k = -\frac{1}{5} \\ b = 30\end{cases}$,
$\therefore$水面高度 h 与流水时间 t 之间的函数关系式为$h = -\frac{1}{5}t + 30$.
(2)当$t = 60$时,$h = -\frac{1}{5} \times 60 + 30 = 18$,
$\therefore$流水时间为 1 h 时,水面高度为 18 cm.
(3)当$h = 0$时,$0 = -\frac{1}{5}t + 30$,$\therefore t = 150$,即经过 150 min,甲容器内的水恰好流完.
查看更多完整答案,请扫码查看


