《2025年时习之暑假衔接八年级数学湘教版》

1. 正比例函数$y = x$的大致图象是()

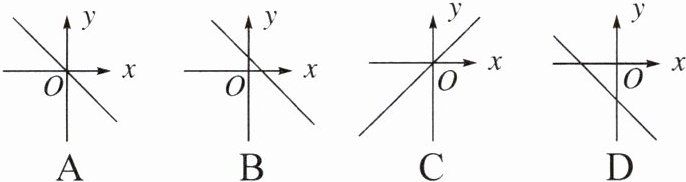
答案： C

2. 一次函数$y = - 2x - 1$的图象不经过()
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： A

3. 若点$A(m, - 1)在函数y = 3x - 7$的图象上,则$m$的值为______.

答案： 2

4. 将直线$y = 4x + 1$向下平移3个单位长度,得到直线______.

答案： y=4x−2

5. 已知一次函数$y = kx + b(k \neq 0)的y随x$的增大而增大,则下列结论中一定正确的是()
A. $k ＜ 0$
B. $k ＞ 0$
C. $b ＜ 0$
D. $b ＞ 0$

答案： B

6. 已知一次函数$y = (m + 2)x + 1$,若$y随x$的增大而增大,则$m$的取值范围是______.

答案： m＞−2

7. 若一次函数$y = kx - 10的图象经过点(2,0)$,则$k$的值为()
A. $- 6$
B. $6$
C. $- 5$
D. $5$

答案： D

8. 已知一次函数$y = ax + b(a,b$为常数,$a \neq 0)经过点(1,3)和(0, - 2)$,则$a - b$的值为()
A. $- 1$
B. $- 3$
C. $3$
D. $7$

答案： D

9. 小明爸爸开车带小明去杭州游玩,一路上匀速前行,小明记下了如下数据：
|观察时刻|$9:00$|$9:06$|$9:18$|(注：“杭州$90km$”表示离杭州的距离为$90km$)|
|----|----|----|----|----|
|路牌内容|杭州$90km$|杭州$80km$|杭州$60km$| |
从$9:00$开始,记汽车行驶的时间为$t(min)$,汽车离杭州的距离为$s(km)$,则$s关于t$的函数表达式为______.

答案： s=90−$\frac{5}{3}$t

10. 已知$y - m与x + n$成正比例(其中$m,n$是常数).
(1)$y是关于x$的一次函数吗？
(2)如果当$y = 1$时,$x = - 2$；当$x = 3$时,$y = 6$,求$y关于x$的函数表达式.

答案： 解：
(1) 是.
(2) 设 $ y - m = k(x + n) $，则$ y = kx + kn + m $.
依题意得$\begin{cases} 1 = -2k + kn + m, \\ 6 = 3k + kn + m, \end{cases} $解得$ \begin{cases} k = 1, \\ n + m = 3. \end{cases}$
$\therefore y = x + 3 $.