2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
7.如图,直角坐标系中四边形ABCD的面积是()
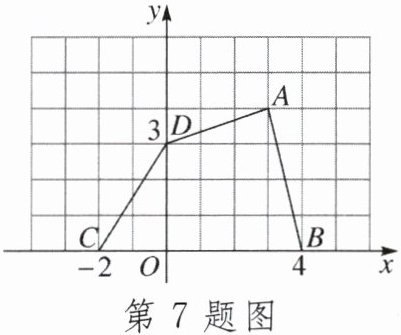
A.15.5
B.20.5
C.26
D.31

A.15.5
B.20.5
C.26
D.31
答案:
A
8.如图,△ABC的顶点坐标分别为A(-1,4),B(-4,-1),C(1,1),则△ABC的面积是____.
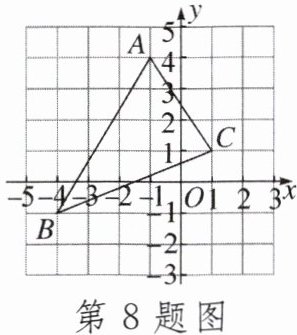

答案:
9.5
9.如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,1),B(4,1),C(4,3),D(2,4),
则四边形ABCD的面积为____.
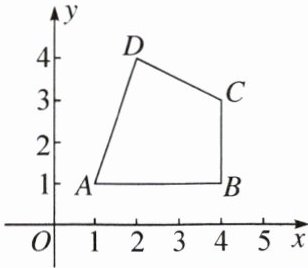
则四边形ABCD的面积为____.

答案:
$\frac{13}{2}$
10.如图所示的平面直角坐标系中,△ABC的顶点分别是A(0,0),B(7,1),C(4,5).
(1)若将△ABC向上平移1个单位长度,再向右平移2个单位长度,得到$△A_1B_1C_1,$则点$A_1$的坐标为____,点$B_1$的坐标为____;
(2)在(1)的条件下,求线段BC扫过的面积.
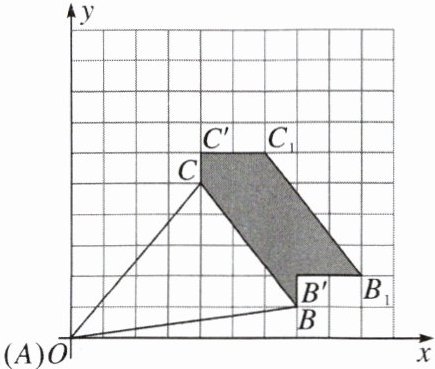
(1)若将△ABC向上平移1个单位长度,再向右平移2个单位长度,得到$△A_1B_1C_1,$则点$A_1$的坐标为____,点$B_1$的坐标为____;
(2)在(1)的条件下,求线段BC扫过的面积.

答案:
解:
(1)(2,1) (9,2)
(2)连接B'C',则线段BC扫过的面积=S▱BB、cc+S▱B'B1C1c=1×3+2×4=11.
(1)(2,1) (9,2)
(2)连接B'C',则线段BC扫过的面积=S▱BB、cc+S▱B'B1C1c=1×3+2×4=11.
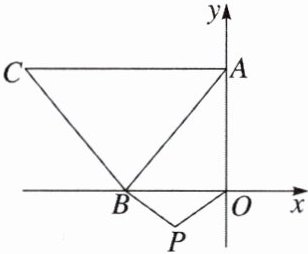
11.如图,在平面直角坐标系中,点A的坐标为(0,a),点B的坐标为(b,0),点C的坐标为(c,a),且a,b,c满足关系式√{a - 3}+|b + 2|$+(c + 4)^2= 0.(1)$请求出A,B,C三点的坐标.
(2)如果在第三象限内有一点P(-1,m),请用含m的式子表示四边形OPBA的面积.
(3)在(2)的条件下,当m= -1时,在x轴上是否存在点M,使三角形ABM的面积等于四边形OPBA面积的3/2? 若存在,请直接写出点M的坐标;若不存在,请说明理由.
(2)如果在第三象限内有一点P(-1,m),请用含m的式子表示四边形OPBA的面积.
(3)在(2)的条件下,当m= -1时,在x轴上是否存在点M,使三角形ABM的面积等于四边形OPBA面积的3/2? 若存在,请直接写出点M的坐标;若不存在,请说明理由.

答案:
解:
(1)
∵$\sqrt{a−3}$+|b+2|+(c+4)²=0,
∴a−3=0,b+2=0,c+4=0.
∴a=3,b=−2,c=−4.
∴点A 的坐标为(0,3),点B的坐标为(−2,0),点C的坐标为(−4,3).
(2)过点P作PE⊥OB于点E,则PE=一m.
∵A(0,3),B(−2,0),
∴AO=3,BO=2.
∴S三角形ABO=$\frac{1}{2}$AO.BO=$\frac{1}{2}$×3×2=3,S三角形BPO= $\frac{1}{2}$BO.PE=$\frac{1}{2}$×2×(−m)=−m.
∴S四边形OPBA= S三角形ABO+S三角形BPO=3+(−m)=3−m.
(3)存在,点M的坐标为(−6,0)或(2,0). 解析:假设存在这样的点M,设M(n,0),则BM=|n+2|. m=−1,
∴S四边形OPBA=3−m=4.
∵S三角形ABM= $\frac{1}{2}$BM.OA=$\frac{1}{2}$|n+2|×3=$\frac{3}{2}$|n+2|,
∴$\frac{3}{2}$|n+2∣=$\frac{3}{2}$×4,解得n=−6或n=2.
∴存在点M,点M 的坐标为(−6,0)或(2,0).
(1)
∵$\sqrt{a−3}$+|b+2|+(c+4)²=0,
∴a−3=0,b+2=0,c+4=0.
∴a=3,b=−2,c=−4.
∴点A 的坐标为(0,3),点B的坐标为(−2,0),点C的坐标为(−4,3).
(2)过点P作PE⊥OB于点E,则PE=一m.
∵A(0,3),B(−2,0),
∴AO=3,BO=2.
∴S三角形ABO=$\frac{1}{2}$AO.BO=$\frac{1}{2}$×3×2=3,S三角形BPO= $\frac{1}{2}$BO.PE=$\frac{1}{2}$×2×(−m)=−m.
∴S四边形OPBA= S三角形ABO+S三角形BPO=3+(−m)=3−m.
(3)存在,点M的坐标为(−6,0)或(2,0). 解析:假设存在这样的点M,设M(n,0),则BM=|n+2|. m=−1,
∴S四边形OPBA=3−m=4.
∵S三角形ABM= $\frac{1}{2}$BM.OA=$\frac{1}{2}$|n+2|×3=$\frac{3}{2}$|n+2|,
∴$\frac{3}{2}$|n+2∣=$\frac{3}{2}$×4,解得n=−6或n=2.
∴存在点M,点M 的坐标为(−6,0)或(2,0).
查看更多完整答案,请扫码查看


