2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
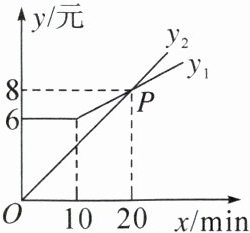
5.共享电动车是一种新理念下的交通工具,主要面向3~10km的出行市场,现有A,B两种品牌的共享电动车,下面图象反映了收费y(元)与骑行时间x(min)之间的对应关系,其中A品牌的收费方式对应$y_{1}$,B品牌的收费方式对应$y_{2}$.请根据相关信息,解答下列问题:
(1)分别求$y_{1}(x≥10),y_{2}$关于x的函数解析式;
(2)如果小明每天早上骑行A品牌或B品牌的共享电动车去上班,已知两种品牌共享电动车的平均行驶速度均为0.3km/min,小明家到公司的距离为9km,那么小明选择____品牌共享电动车更省钱;(填“A”或“B”)
(3)当x为何值时,两种品牌共享电动车收费相差4元?
(1)分别求$y_{1}(x≥10),y_{2}$关于x的函数解析式;
(2)如果小明每天早上骑行A品牌或B品牌的共享电动车去上班,已知两种品牌共享电动车的平均行驶速度均为0.3km/min,小明家到公司的距离为9km,那么小明选择____品牌共享电动车更省钱;(填“A”或“B”)
(3)当x为何值时,两种品牌共享电动车收费相差4元?

答案:
解:
(1)当$x\geq10$时,设$y_1 = kx + b$,
将$(10,6)$和$(20,8)$分别代入$y_1 = kx + b$,得$\begin{cases}10k + b = 6,\\20k + b = 8,\end{cases}$解得$\begin{cases}k = 0.2,\\b = 4,\end{cases}$$\therefore$
当$x\geq10$时,$y_1 = 0.2x + 4$.
$\because B$品牌每分钟收费$8\div20 = 0.4$(元),
$\therefore y_2 = 0.4x(x\geq0)$.
答:$y_1$关于$x$的函数解析式为$y_1 = 0.2x + 4(x\geq10)$,$y_2$
关于$x$的函数解析式为$y_2 = 0.4x(x\geq0)$.
(2)$A$
(3)当$0\leq x < 10$时,$|y_1 - y_2| = |6 - 0.4x| = 4$,解得$x = 5$或$x = 25$(舍去);
当$x\geq10$时,$|y_1 - y_2| = |0.2x + 4 - 0.4x| = 4$,解得$x = 0$(舍去)或$x = 40$.
$\therefore x = 5$或 40.
答:当$x$为 5 或 40 时,两种品牌共享电动车收费相差 4 元.
(1)当$x\geq10$时,设$y_1 = kx + b$,
将$(10,6)$和$(20,8)$分别代入$y_1 = kx + b$,得$\begin{cases}10k + b = 6,\\20k + b = 8,\end{cases}$解得$\begin{cases}k = 0.2,\\b = 4,\end{cases}$$\therefore$
当$x\geq10$时,$y_1 = 0.2x + 4$.
$\because B$品牌每分钟收费$8\div20 = 0.4$(元),
$\therefore y_2 = 0.4x(x\geq0)$.
答:$y_1$关于$x$的函数解析式为$y_1 = 0.2x + 4(x\geq10)$,$y_2$
关于$x$的函数解析式为$y_2 = 0.4x(x\geq0)$.
(2)$A$
(3)当$0\leq x < 10$时,$|y_1 - y_2| = |6 - 0.4x| = 4$,解得$x = 5$或$x = 25$(舍去);
当$x\geq10$时,$|y_1 - y_2| = |0.2x + 4 - 0.4x| = 4$,解得$x = 0$(舍去)或$x = 40$.
$\therefore x = 5$或 40.
答:当$x$为 5 或 40 时,两种品牌共享电动车收费相差 4 元.
6.根据以下活动项目提供的材料,完成相关任务.
【活动主题】怎样确定巡航船接收信号的有效时长?
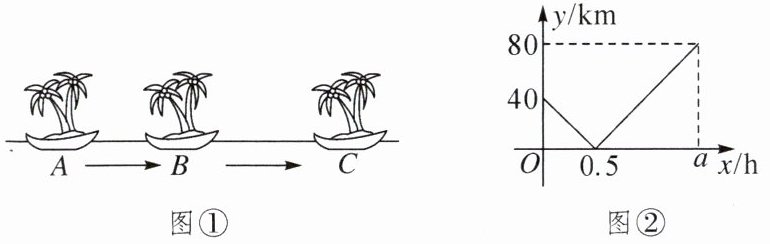
【活动过程】素材1:如图①,A,B,C三个海岛在同一条直线上,巡航船从A岛出发沿直线行驶,航行速度一直保持不变,经过B岛驶向C岛,执行巡航任务.
素材2:B岛处有一个不间断发射信号的发射台,发射信号的覆盖半径为30km.
素材3:设该巡航船行驶的时间为x(h),与B岛的距离为y(km),y与x的函数关系的图象如图②所示.
【问题解决】
(1)A岛与C岛之间的距离为____km,$a= $____.
(2)直接写出y与x之间的函数关系式;
(3)试确定该巡航船接收信号的有效时长.
【活动主题】怎样确定巡航船接收信号的有效时长?
【活动过程】素材1:如图①,A,B,C三个海岛在同一条直线上,巡航船从A岛出发沿直线行驶,航行速度一直保持不变,经过B岛驶向C岛,执行巡航任务.
素材2:B岛处有一个不间断发射信号的发射台,发射信号的覆盖半径为30km.
素材3:设该巡航船行驶的时间为x(h),与B岛的距离为y(km),y与x的函数关系的图象如图②所示.
【问题解决】
(1)A岛与C岛之间的距离为____km,$a= $____.
(2)直接写出y与x之间的函数关系式;
(3)试确定该巡航船接收信号的有效时长.

答案:
解:
(1)120 1.5
(2)$y = \begin{cases}-80x + 40(0\leq x\leq0.5),\\80x - 40(0.5 < x\leq1.5).\end{cases}$
(3)在$y = -80x + 40$中,令$y = 30$,得$30 = -80x + 40$,解得$x = \frac{1}{8}$;
在$y = 80x - 40$中,令$y = 30$,得$30 = 80x - 40$,解得$x = \frac{7}{8}$.
$\because\frac{7}{8} - \frac{1}{8} = \frac{3}{4}(h)$,
$\therefore$该巡航船接收信号的有效时长为$\frac{3}{4}h$.
(1)120 1.5
(2)$y = \begin{cases}-80x + 40(0\leq x\leq0.5),\\80x - 40(0.5 < x\leq1.5).\end{cases}$
(3)在$y = -80x + 40$中,令$y = 30$,得$30 = -80x + 40$,解得$x = \frac{1}{8}$;
在$y = 80x - 40$中,令$y = 30$,得$30 = 80x - 40$,解得$x = \frac{7}{8}$.
$\because\frac{7}{8} - \frac{1}{8} = \frac{3}{4}(h)$,
$\therefore$该巡航船接收信号的有效时长为$\frac{3}{4}h$.
查看更多完整答案,请扫码查看


