2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1.父亲告诉小明:“距离地面越高,温度越低.”并且出示了下面的表格:
|距离地面高度(千米)|0|1|2|3|4|5|
|----|----|----|----|----|----|----|
|温度(℃)|20|14|8|2|-4|-10|
那么根据表格中的规律,距离地面6千米的高空温度是()
A.-10℃
B.-16℃
C.-18℃
D.-20℃
|距离地面高度(千米)|0|1|2|3|4|5|
|----|----|----|----|----|----|----|
|温度(℃)|20|14|8|2|-4|-10|
那么根据表格中的规律,距离地面6千米的高空温度是()
A.-10℃
B.-16℃
C.-18℃
D.-20℃
答案:
B
2.今年劳动节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是()
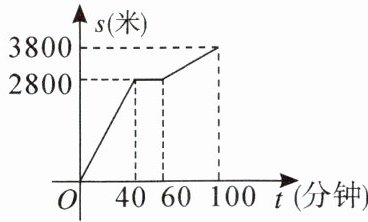
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
答案:
C
3.如图①,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图②中的线段AB,CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是()

A.注水前乙容器内水的高度是5厘米
B.甲容器内的水4分钟全部注入乙容器
C.注水2分钟时,甲、乙两个容器中的水的深度相等
D.注水1分钟时,甲容器的水比乙容器的水深5厘米

A.注水前乙容器内水的高度是5厘米
B.甲容器内的水4分钟全部注入乙容器
C.注水2分钟时,甲、乙两个容器中的水的深度相等
D.注水1分钟时,甲容器的水比乙容器的水深5厘米
答案:
D
4.假定甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系在平面直角坐标系中如图所示,请结合图
象回答问题:甲到达终点时,乙离终点还有______米.
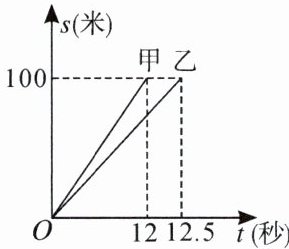
象回答问题:甲到达终点时,乙离终点还有______米.

答案:
4
5.某市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种、B种树木每棵各多少元.
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价八折优惠,请设计一种购买树木的方案,使实际所花费用最少,并求出最少的费用.
(1)求A种、B种树木每棵各多少元.
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价八折优惠,请设计一种购买树木的方案,使实际所花费用最少,并求出最少的费用.
答案:
解:
(1)设 A 种树木每棵 x 元,B 种树木每棵 y 元.依题意得$\begin{cases}2x + 5y = 600 \\ 3x + y = 380\end{cases}$,解得$\begin{cases}x = 100 \\ y = 80\end{cases}$
答:A 种树木每棵 100 元,B 种树木每棵 80 元.
(2)设购买 A 种树木为 a 棵,则购买 B 种树木为$(100 - a)$棵.
由题意得$a \geq 3(100 - a)$,解得$a \geq 75$.
设实际付款总金额是 w 元,则$w = 0.8[100a + 80(100 - a)]$,即$w = 16a + 6400$.
$\because 16 > 0$,w 随 a 的增大而增大,
$\therefore$当$a = 75$时,w 最小,$w_{最小值} = 16 \times 75 + 6400 = 7600$.
答:当购买 A 种树木 75 棵,B 种树木 25 棵时,所需费用最少,最少费用为 7600 元.
(1)设 A 种树木每棵 x 元,B 种树木每棵 y 元.依题意得$\begin{cases}2x + 5y = 600 \\ 3x + y = 380\end{cases}$,解得$\begin{cases}x = 100 \\ y = 80\end{cases}$
答:A 种树木每棵 100 元,B 种树木每棵 80 元.
(2)设购买 A 种树木为 a 棵,则购买 B 种树木为$(100 - a)$棵.
由题意得$a \geq 3(100 - a)$,解得$a \geq 75$.
设实际付款总金额是 w 元,则$w = 0.8[100a + 80(100 - a)]$,即$w = 16a + 6400$.
$\because 16 > 0$,w 随 a 的增大而增大,
$\therefore$当$a = 75$时,w 最小,$w_{最小值} = 16 \times 75 + 6400 = 7600$.
答:当购买 A 种树木 75 棵,B 种树木 25 棵时,所需费用最少,最少费用为 7600 元.
查看更多完整答案,请扫码查看


