《2025年时习之暑假衔接八年级数学湘教版》

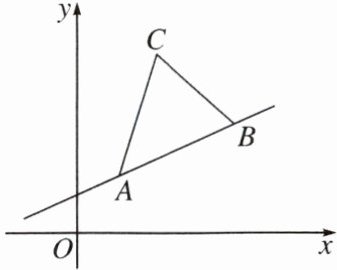
1. 如图,直线$y = \frac{1}{2}x + 1经过点A(1,m)$,$B(4,n)$,点$C的坐标为(2,5)$,求$\triangle ABC$的面积.

答案：
解:如图，作$CM⊥x$轴于$M$，交$AB$于$D$。$∵$点$C$的坐标为$(2,5)$，$∴D$的横坐标为$2$。把$x=2$代入直线$y=\frac{1}{2}x+1$，得$y=\frac{1}{2}×2+1=2$，$∴D(2,2)$。$∴CD=5-2=3$。$∴S_{\triangle ABC}=S_{\triangle ACD}+S_{\triangle BCD}=\frac{1}{2}×3×(4-1)=\frac{9}{2}$。

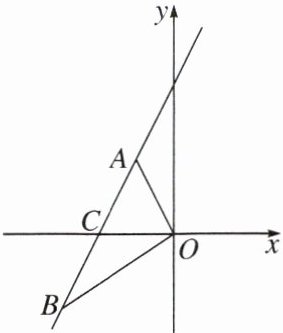
2. 如图,已知一次函数$y = kx + b(k \neq 0)的图象过点A(-1,2)$,$B(m,-2)$,与$x轴交于点C(-2,0)$,连接$OA$,$OB$.
(1)求该一次函数的解析式和$m$的值.
(2)若点$P为y$轴上的点,是否存在点$P$,使得$S_{\triangle OBP} = S_{\triangle AOB}$?若存在,请求出所有符合条件的点$P$的坐标;若不存在,请说明理由.

答案： 解:
(1)
∵点$A(-1,2)$，$C(-2,0)$在一次函数$y=kx+b(k≠0)$的图象上，$∴\begin{cases}-k+b=2\\-2k+b=0\end{cases}$，解得$\begin{cases}k=2\\b=4\end{cases}$。$∴$一次函数的解析式为$y=2x+4$。$∵B(m,-2)$在函数的图象上，$∴2m+4=-2$，解得$m=-3$。
(2)存在。$∵A(-1,2)$，$B(-3,-2)$，$C(-2,0)$，$∴S_{\triangle AOB}=S_{\triangle AOC}+S_{\triangle BOC}=\frac{1}{2}×2×2+\frac{1}{2}×2×2=2+2=4$。当点$P$在$y$轴上时，设$P(0,n)$，则$S_{\triangle OBP}=\frac{1}{2}|n|×3=4$，解得$n=±\frac{8}{3}$。$∴$点$P$的坐标为$(0,\frac{8}{3})$或$(0,-\frac{8}{3})$。

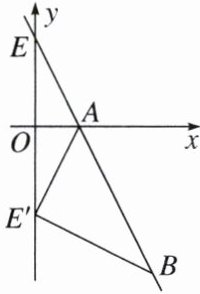
3. 如图,直线$l:y = -2x + 6分别交x$轴、$y轴于点A$,$E$,点$B(m,-10)在直线l$上,点$E关于x轴的对称点为E'$,连接$AE'$,$BE'$.
(1)求点$A$的坐标;
(2)求$\triangle ABE'$的面积;
(3)点$Q(1,a)$为平面内一动点,连接$QA$,$QE'$,若$S_{\triangle QAE'} = \frac{1}{2}S_{\triangle ABE'}$,求点$Q$的坐标.

答案：
解:
(1)在直线$y=-2x+6$中，令$y=0$，则$x=3$。$∴A(3,0)$。
(2)由题意可知$E(0,6)$，$E'(0,-6)$，$∴EE'=12$。$∵$点$B(m,-10)$在$y=-2x+6$上，$∴-2m+6=-10$，解得$m=8$。$∴B(8,-10)$。$∴S_{\triangle ABE'}=S_{\triangle EBE'}-S_{\triangle EAE'}=\frac{1}{2}EE'×8-\frac{1}{2}EE'×3=\frac{1}{2}×12×(8-3)=30$。
(3)如图，作$QF// y$轴交$AE'$于点$F$。由题意可知直线$AE'$的表达式为$y=2x-6$，当$x=1$时，$y=-4$，$∴F(1,-4)$。$∵S_{\triangle QAE'}=\frac{1}{2}S_{\triangle ABE'}=15$，$∴\frac{1}{2}QF×(3-1)+\frac{1}{2}QF×1=15$。$∴QF=10$。$∴|a+4|=10$，解得$a=6$或$a=-14$。$∴$点$Q$的坐标为$(1,6)$或$(1,-14)$。