2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
某校八年级学生在数学课上进行了项目化学习研究,某小组研究如下:
【提出驱动性问题】越来越多的人选择通过快递公司代办点邮寄包裹,那么选择哪家快递公司更合算呢?
【设计实践任务】根据“素材1”“素材2”,设计了“任务1”“任务2”“任务3”的实践活动。请你尝试帮助他们解决相关问题。
|选择更优惠的快递公司|
|----|
|素材1|甲、乙两个快递代办点省外邮寄费用标准如下:甲:首重1kg收费8元,续重5元/kg;(即所寄物品质量不超过1kg时收费8元,质量超过1kg时超过部分按每千克加收5元计费)乙:首重1kg收费10元,续重3元/kg。|
|素材2|快递代办点所寄物品的快递费用y(元)与物品质量x(kg)之间存在函数关系,关系式为$y_{甲}= \left\{\begin{array}{l} 8(0\lt x\leqslant1),\\ 5x+3(x\gt1),\end{array}\right. $
$y_{乙}= ?$,其中,$y_{甲}$的函数图象如图所示。|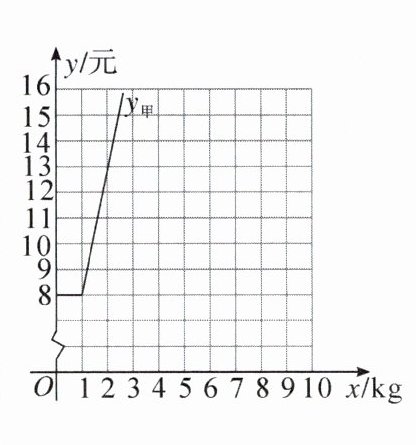
|问题解决|
|任务1|建立模型|求$y_{乙}$与x之间的函数关系式。|
|任务2|绘制图象|在图中画出$y_{乙}$的函数图象。|
|任务3|解决问题|根据图象推断哪个快递代办点更优惠。|
【提出驱动性问题】越来越多的人选择通过快递公司代办点邮寄包裹,那么选择哪家快递公司更合算呢?
【设计实践任务】根据“素材1”“素材2”,设计了“任务1”“任务2”“任务3”的实践活动。请你尝试帮助他们解决相关问题。
|选择更优惠的快递公司|
|----|
|素材1|甲、乙两个快递代办点省外邮寄费用标准如下:甲:首重1kg收费8元,续重5元/kg;(即所寄物品质量不超过1kg时收费8元,质量超过1kg时超过部分按每千克加收5元计费)乙:首重1kg收费10元,续重3元/kg。|
|素材2|快递代办点所寄物品的快递费用y(元)与物品质量x(kg)之间存在函数关系,关系式为$y_{甲}= \left\{\begin{array}{l} 8(0\lt x\leqslant1),\\ 5x+3(x\gt1),\end{array}\right. $
$y_{乙}= ?$,其中,$y_{甲}$的函数图象如图所示。|

|问题解决|
|任务1|建立模型|求$y_{乙}$与x之间的函数关系式。|
|任务2|绘制图象|在图中画出$y_{乙}$的函数图象。|
|任务3|解决问题|根据图象推断哪个快递代办点更优惠。|
答案:
解:任务1:根据题意,当$0 < x \leq 1$时,$y_{乙} = 10$;当$x > 1$时,$y_{乙} = 10 + 3(x - 1) = 3x + 7$.$\therefore y_{乙} = \begin{cases} 10(0 < x \leq 1), \\ 3x + 7(x > 1). \end{cases}$
@@任务2:当$x = 1$时,$y_{乙} = 10$,当$x = 2$时,$y_{乙} = 3 \times 2 + 7 = 13$,画出函数图象如下: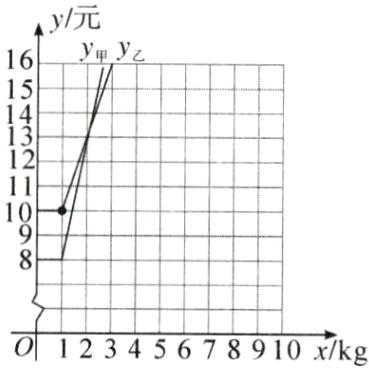
@@任务3:由图象可知,当$0 < x < 2$时,甲快递代办点更优惠;当$x = 2$时,两个快递代办点收费相同;当$x > 2$时,乙快递代办点更优惠.
解:任务1:根据题意,当$0 < x \leq 1$时,$y_{乙} = 10$;当$x > 1$时,$y_{乙} = 10 + 3(x - 1) = 3x + 7$.$\therefore y_{乙} = \begin{cases} 10(0 < x \leq 1), \\ 3x + 7(x > 1). \end{cases}$
@@任务2:当$x = 1$时,$y_{乙} = 10$,当$x = 2$时,$y_{乙} = 3 \times 2 + 7 = 13$,画出函数图象如下:

@@任务3:由图象可知,当$0 < x < 2$时,甲快递代办点更优惠;当$x = 2$时,两个快递代办点收费相同;当$x > 2$时,乙快递代办点更优惠.
查看更多完整答案,请扫码查看


