2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 若关于$x的一元一次方程kx + b = 0的解是x = 1$,则直线$y = kx + b与x$轴的交点坐标是()
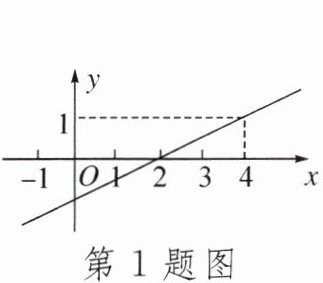
A. $(1, 0)$
B. $(0, 1)$
C. $(0, 0)$
D. $(-1, 0)$

A. $(1, 0)$
B. $(0, 1)$
C. $(0, 0)$
D. $(-1, 0)$
答案:
A
2. 数形结合是解决数学问题常用的思想方法.如图,直线$y = x + 5和直线y = ax + b相交于点P$,根据图象可知,方程$x + 5 = ax + b$的解是()
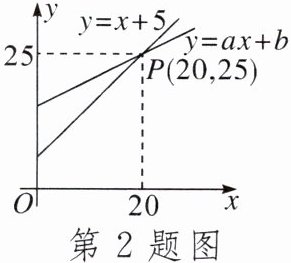
A. $x = 20$
B. $x = 5$
C. $x = 25$
D. $x = 15$

A. $x = 20$
B. $x = 5$
C. $x = 25$
D. $x = 15$
答案:
A
3. 如图,直线$y = kx + b(k < 0)经过点P(1, 1)$,当$kx + b \geq x$时,$x$的取值范围为()
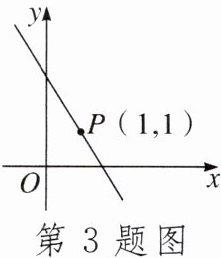
A. $x \leq 1$
B. $x \geq 1$
C. $x < 1$
D. $x > 1$

A. $x \leq 1$
B. $x \geq 1$
C. $x < 1$
D. $x > 1$
答案:
A
4. 若方程组$\begin{cases}x + y = 2,\\2x + 2y = 3\end{cases}$没有解,则一次函数$y = 2 - x与y = \frac{3}{2} - x$的图象必定()
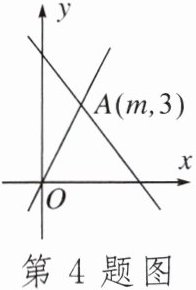
A. 重合
B. 平行
C. 相交
D. 无法确定
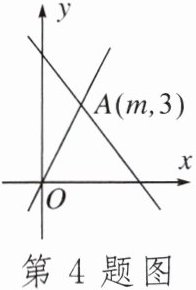
A. 重合
B. 平行
C. 相交
D. 无法确定
答案:
B
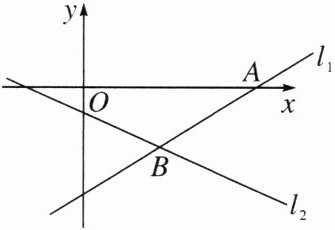
5. 如图,直线$l_2的解析式为y = -\frac{1}{4}x - 1$,直线$l_1过点A(8, 0)$,且与直线$l_2相交于点B$,$B的横坐标为4$.
(1)求点$B$的坐标;
(2)点$B$的坐标可看作是哪个二元一次方程组的解?
(1)求点$B$的坐标;
(2)点$B$的坐标可看作是哪个二元一次方程组的解?

答案:
解:
(1)当x=4时,y=−$\frac{1}{4}$×4−1=−2,
∴点B的坐标为(4,−2).
(2)设直线l1的解析式为y=kx+b,把A(8,0),B(4,−2)代入得$\left\{\begin{array}{l} 8k+b=0,\\ 4k+b=-2,\end{array}\right. $解得$\left\{\begin{array}{l} k=\frac {1}{2},\\ b=-4.\end{array}\right. $
∴直线l1的解析式为y=$\frac{1}{2}$x−4.
∴点B的坐标可看作是二元一次方程组$\left\{\begin{array}{l} y=-\frac {1}{4}x-1,\\ y=\frac {1}{2}x-4\end{array}\right. $的解.
(1)当x=4时,y=−$\frac{1}{4}$×4−1=−2,
∴点B的坐标为(4,−2).
(2)设直线l1的解析式为y=kx+b,把A(8,0),B(4,−2)代入得$\left\{\begin{array}{l} 8k+b=0,\\ 4k+b=-2,\end{array}\right. $解得$\left\{\begin{array}{l} k=\frac {1}{2},\\ b=-4.\end{array}\right. $
∴直线l1的解析式为y=$\frac{1}{2}$x−4.
∴点B的坐标可看作是二元一次方程组$\left\{\begin{array}{l} y=-\frac {1}{4}x-1,\\ y=\frac {1}{2}x-4\end{array}\right. $的解.
请根据学习“一次函数”时积累的经验和方法研究函数$y = -|x| + 2$的图象和性质,并解决问题.
(1)填空:
①当$x = 0$时,$y = -|x| + 2 = $______;
②当$x > 0$时,$y = -|x| + 2 = $______;
③当$x < 0$时,$y = -|x| + 2 = $______.
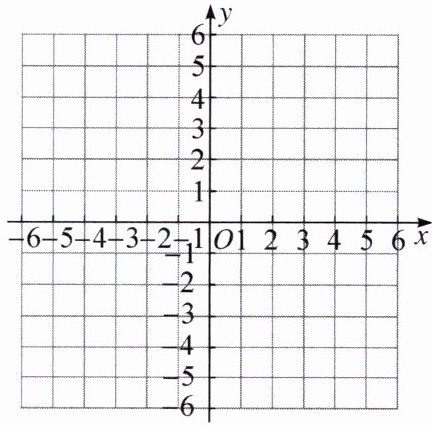
(2)在平面直角坐标系中作出函数$y = -|x| + 2$的图象.
| $x$ | … | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | … |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| $y$ | … | $-1$ | $0$ | $1$ | $2$ | $1$ | $0$ | $-1$ | … |
(3)进一步探究函数图象发现:
①函数图象与$x$轴有______个交点,方程$-|x| + 2 = 0$有______个解;
②方程$-|x| + 2 = 2$有______个解;
③若关于$x的方程-|x| + 2 = a$无解,则$a$的取值范围是______.
(1)填空:
①当$x = 0$时,$y = -|x| + 2 = $______;
②当$x > 0$时,$y = -|x| + 2 = $______;
③当$x < 0$时,$y = -|x| + 2 = $______.
(2)在平面直角坐标系中作出函数$y = -|x| + 2$的图象.

| $x$ | … | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | … |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| $y$ | … | $-1$ | $0$ | $1$ | $2$ | $1$ | $0$ | $-1$ | … |
(3)进一步探究函数图象发现:
①函数图象与$x$轴有______个交点,方程$-|x| + 2 = 0$有______个解;
②方程$-|x| + 2 = 2$有______个解;
③若关于$x的方程-|x| + 2 = a$无解,则$a$的取值范围是______.
答案:
解:
(1)①2 ②−x+2 ③x+2
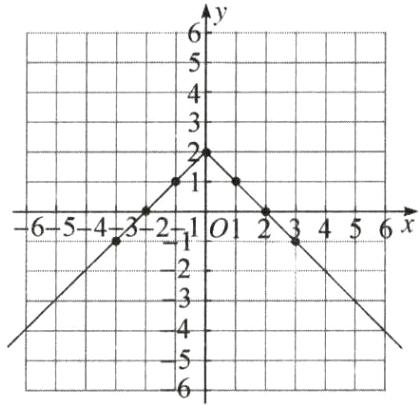
(2)函数y=−|x|+2的图象如图所示.
(3)①2 2 ②1 ③a>2
解:
(1)①2 ②−x+2 ③x+2
(2)函数y=−|x|+2的图象如图所示.

(3)①2 2 ②1 ③a>2
查看更多完整答案,请扫码查看


