《2025年时习之暑假衔接八年级数学湘教版》

1.在平面直角坐标系中,对于点$P(a,b)$,我们把点$P_{1}(b+1,1-a)叫作点P$的友谊点.已知点$M_{1}的友谊点为M_{2}$,点$M_{2}的友谊点为M_{3}$,点$M_{3}的友谊点为M_{4}$……这样依次得到点$M_{1}$,$M_{2}$,$M_{3}$,…$$,$M_{n}$.若点$M_{1}的坐标为(2,3)$,则点$M_{2025}$的坐标为()
A.$(0,-3)$
B.$(2,3)$
C.$(4,-1)$
D.$(-2,1)$

答案： B

2.如图,在平面直角坐标系中,$A(1,1)$,$B(-1,1)$,$C(-1,-2)$,$D(1,-2)$,把一条长为2025个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点$A$处,并按$A-B-C-D-A……的规律绕在四边形ABCD$的边上,则细线另一端所在位置的点的坐标是()

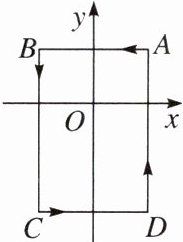
A.$(-1,0)$
B.$(0,1)$
C.$(-1,-2)$
D.$(1,-1)$

答案： C

3.如图,在$x轴的正半轴与射线AB$上各放置着一平面镜,$AB// x$轴,发光点$(0,1)$处沿如图所示的方向发射一束光,每当碰到镜面时会反射(反射时反射角等于入射角),当光线第30次碰到镜面时的坐标为()

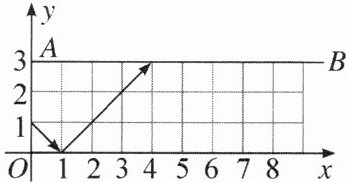
A.$(30,3)$
B.$(88,3)$
C.$(30,0)$
D.$(88,0)$

答案： B　解析:由题意可得出经过第一次反射到点(1,0)，经过第二次反射到点(4，3)，经过第三次反射到点(7，0)，经过第四次反射到点(10,3)……故当反射次数为偶数时，点在射线AB上，纵坐标是3，横坐标依次加6,则当光线第2n(n为整数)次碰到镜面时，纵坐标为3,横坐标为6n−2.当光线第30次碰到镜面时，纵坐标为3,横坐标为6×15−2=88..
∴当光线第30次碰到镜面时的坐标为(88,3).故选B.

4.如图,点$A_{1}(1,1)$向上平移1个单位,再向右平移2个单位,得到点$A_{2}$;点$A_{2}$向上平移2个单位,再向右平移4个单位,得到点$A_{3}$;点$A_{3}$向上平移4个单位,再向右平移8个单位,得到点$A_{4}……按这个规律平移得到点A_{100}$,则点$A_{100}$的坐标为()

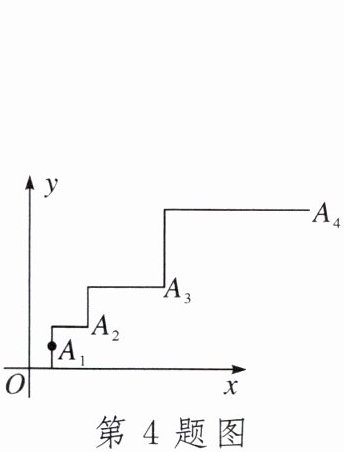
A.$(2^{100}-1,2^{100})$
B.$(2^{99},2^{100})$
C.$(2^{100}-1,2^{99})$
D.$(2^{99}+1,2^{100})$

答案： 4.C　解析:由题意知，点A1的坐标为(1,1),点A2的坐标为(3,2)，点A3的坐标为(7,4)，点A4的坐标为(15，8),..,，由此可见，点A，的横坐标可表示为2”-1,纵坐标可表示为2"−1(n为正整数).当n=100时，点A100的坐标为(2100−1,2").故选C.

5.在平面直角坐标系中,直线$l经过点A(0,-1)$,点$A_{1}$,$A_{2}$,$A_{3}$,$A_{4}$,$A_{5}$,$A_{6}…$均为格点,且按如图所示的规律排列在直线$l$上,若点$A_{n}的纵坐标为-2025$,则$n$的值为()

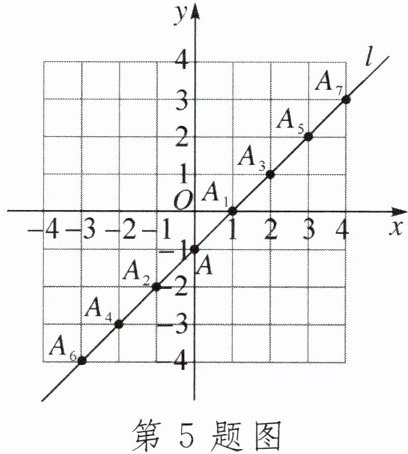
A.4046
B.4047
C.4048
D.4049

答案： 5.C　解析:各格点的坐标为A1(1,0),A2(−1,−2)，
A3(2,1),A4(−2,−3),A5(3,2),A6(−3,−4),
A7(4,3)..根据规律，奇数格点的坐标为A2m+1(m+1,m),m=0,1,2...;偶数格点的坐标为A2k+2(一k-1,−k−2),k=0,1,2....
∵点A的纵坐标为−2025，
∴A为偶数格点.
∴−2025=−k−2,解得k=2023.
∴n=2k+2=2023×2+2=4048.故选C.