2025年奔跑吧少年九年级语文全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级语文全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
为参与学校文学社组织的诗歌创作活动,同学们搜集了资料,以下是两个小组的汇报。请你聆听汇报并完成下列任务。(12分)
〔甲组汇报〕
①我们小组重点研读了中国科学院院士严加安的《数学如诗 境界为上》等文章,围绕“数学与诗歌的共性”搜集了如下材料。
②第一,数学与诗歌的源泉都是自然与社会。宋代大诗人陆游告诫儿子说:“汝果欲学诗,工夫在诗外。”这个“诗外”就是诗人对日常生活和大自然细致的观察、体验、感知,这是诗歌创作的源泉。做数学研究也与诗歌创作类似,数学史家傅立叶认为:“对自然的深入研究是数学发现的最富饶的源泉。”
③第二,数学和诗歌都追求和谐与简洁。诗歌力图通过简洁的语言和和谐的韵律,抒发诗人的情怀,表达深邃的哲理。数学的和谐是不言而喻的。至于数学的简洁,一方面,数学结果是通过简明的命题或定理的形式来表述的;另一方面,在研究过程中,数学家追求在较少条件下推出尽可能广泛而深刻的结论,或者力图简化已有结果的证明。
④第三,数学中的“对偶”与诗歌中的“对仗”异曲同工。诗歌中的“对仗”能够使意境更加优美,抒情更加感人。数学中的“对偶”使得数学理论变得更加深刻,更加优美。数学中的“对偶”不只是数学的结构和框架,而且是一种思维方式,也是重要的证明工具和技巧。
⑤第四,数学和诗歌的创作都需要丰富的直觉和想象。如李白《望庐山瀑布》中的诗句“飞流直下三千尺,疑是银河落九天”就极富直觉和想象,这种直觉和想象源于诗人的形象思维。有人说:“一个数学家必须要具有诗人的气质。”一个数学家不一定要写诗,但是气质要像诗人,即要有丰富的直觉和想象,这样才能做好数学研究。
〔乙组汇报〕
①我们小组阅读了刘福智教授的《数学与诗》,他强调:数学的特点决定了数学形式的简洁性,简洁性是美的特性。大千世界纷繁富丽,气象万千,在庞杂无序的自然现象中抽象出数学概念,凝结为数学形式,反过来解释并统摄更多的现象,这正是数学的功能和威力所在,也是简洁之美的体现。世界上恐怕存在着无数个三角形,千状万端,难以想象。当初人们在获得了长方形面积的计算方法而还不知道三角形的面积如何计算的时候,大概谁也不会想到方法是如此简单:$S= \frac{1}{2}ah$($a$为三角形的底边,$h$为底边上的高)。这个公式适用于任何三角形,并能据此推出所有多边形的面积公式。形式是那么简单,而应用又是如此广泛。可以说,所有的数学公式、物理学公式、化学公式都是无数科学现象的高度凝聚,都是简洁之美的结晶。
②而在文学领域中,诗歌堪称简洁美的典范。为了简洁,有的科学家手里捏着一把剃刀,而有的文学家,甚至是拿着“一把斧”。海明威就是这样。海明威作品的简洁风格对于20世纪的文学产生过重要影响。有人说,他是一位手里“拿着一把斧”的作家,他“斩伐了整座森林的冗言赘语,还原了基本枝干的清爽面目”“删节了解释、探讨甚至议论;砍掉了一切花花绿绿的比喻,清除了古老神圣、毫无生气的文章俗套”。海明威主张依照所谓“冰山原理”去写作。轮船在高纬度海面上会遇到巨大的冰山,而冰山在海面下的部分更为巨大,是整座冰山的十分之九。所谓“冰山原理”,就是作家要借助能见到的十分之一,暗示见不到的十分之九。“冰山原理”在诗歌创作中也同样适用。诗歌通过跳跃,精选尽可能少的文字表现尽可能多的内涵。这就是古人所说的“言简而意丰”和“言有尽而意无穷”。
(均根据相关材料改编)
19. 跨学科 数学 甲、乙两个小组汇报的观点之间是什么关系?下列图示中,最能体现这种关系的一项是
(

20. 甲组汇报中多处引用诗句作为材料证明观点。请选择我们学过的诗词,为汇报中的画线句子提供合适的论据,并加以简要分析,论证它的观点。(3分)
21. 从甲、乙两组中选择一组,结合“论证要合理”评价量表,任选两个角度,对该组所搜集的材料进行评价。(4分)
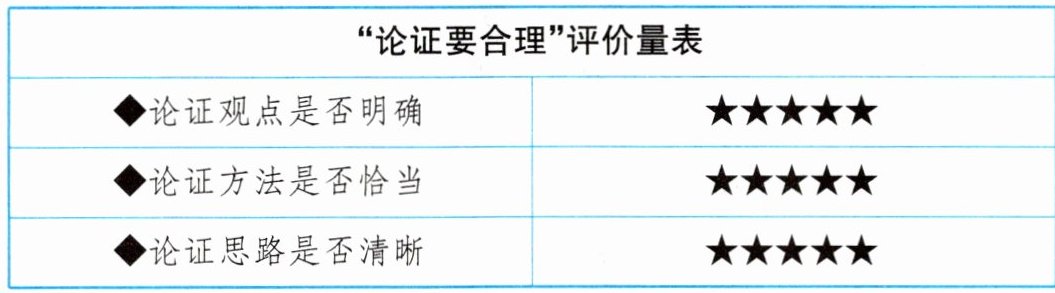
示例:甲组。
论证观点明确:围绕“数学与诗歌的共性”展开论述,观点清晰。
论证方法恰当:引用陆游、傅立叶等人的言论,运用举例论证(李白诗句)等,增强说服力。
22. 微写作 诗歌创作 请以“数学”为话题,参照下面的示例,参与文学社的诗歌创作征稿活动。要求:题目自拟,创作小诗,体现数学相关概念与生活的联系,不超过8行。(3分)

《平行线与生活》
生活如平行线
看似永不相交
却各自延伸
向着远方蔓延
虽无交集的点
却有相同的信念
在各自的轨迹
绽放独特的光焰
〔甲组汇报〕
①我们小组重点研读了中国科学院院士严加安的《数学如诗 境界为上》等文章,围绕“数学与诗歌的共性”搜集了如下材料。
②第一,数学与诗歌的源泉都是自然与社会。宋代大诗人陆游告诫儿子说:“汝果欲学诗,工夫在诗外。”这个“诗外”就是诗人对日常生活和大自然细致的观察、体验、感知,这是诗歌创作的源泉。做数学研究也与诗歌创作类似,数学史家傅立叶认为:“对自然的深入研究是数学发现的最富饶的源泉。”
③第二,数学和诗歌都追求和谐与简洁。诗歌力图通过简洁的语言和和谐的韵律,抒发诗人的情怀,表达深邃的哲理。数学的和谐是不言而喻的。至于数学的简洁,一方面,数学结果是通过简明的命题或定理的形式来表述的;另一方面,在研究过程中,数学家追求在较少条件下推出尽可能广泛而深刻的结论,或者力图简化已有结果的证明。
④第三,数学中的“对偶”与诗歌中的“对仗”异曲同工。诗歌中的“对仗”能够使意境更加优美,抒情更加感人。数学中的“对偶”使得数学理论变得更加深刻,更加优美。数学中的“对偶”不只是数学的结构和框架,而且是一种思维方式,也是重要的证明工具和技巧。
⑤第四,数学和诗歌的创作都需要丰富的直觉和想象。如李白《望庐山瀑布》中的诗句“飞流直下三千尺,疑是银河落九天”就极富直觉和想象,这种直觉和想象源于诗人的形象思维。有人说:“一个数学家必须要具有诗人的气质。”一个数学家不一定要写诗,但是气质要像诗人,即要有丰富的直觉和想象,这样才能做好数学研究。
〔乙组汇报〕
①我们小组阅读了刘福智教授的《数学与诗》,他强调:数学的特点决定了数学形式的简洁性,简洁性是美的特性。大千世界纷繁富丽,气象万千,在庞杂无序的自然现象中抽象出数学概念,凝结为数学形式,反过来解释并统摄更多的现象,这正是数学的功能和威力所在,也是简洁之美的体现。世界上恐怕存在着无数个三角形,千状万端,难以想象。当初人们在获得了长方形面积的计算方法而还不知道三角形的面积如何计算的时候,大概谁也不会想到方法是如此简单:$S= \frac{1}{2}ah$($a$为三角形的底边,$h$为底边上的高)。这个公式适用于任何三角形,并能据此推出所有多边形的面积公式。形式是那么简单,而应用又是如此广泛。可以说,所有的数学公式、物理学公式、化学公式都是无数科学现象的高度凝聚,都是简洁之美的结晶。
②而在文学领域中,诗歌堪称简洁美的典范。为了简洁,有的科学家手里捏着一把剃刀,而有的文学家,甚至是拿着“一把斧”。海明威就是这样。海明威作品的简洁风格对于20世纪的文学产生过重要影响。有人说,他是一位手里“拿着一把斧”的作家,他“斩伐了整座森林的冗言赘语,还原了基本枝干的清爽面目”“删节了解释、探讨甚至议论;砍掉了一切花花绿绿的比喻,清除了古老神圣、毫无生气的文章俗套”。海明威主张依照所谓“冰山原理”去写作。轮船在高纬度海面上会遇到巨大的冰山,而冰山在海面下的部分更为巨大,是整座冰山的十分之九。所谓“冰山原理”,就是作家要借助能见到的十分之一,暗示见不到的十分之九。“冰山原理”在诗歌创作中也同样适用。诗歌通过跳跃,精选尽可能少的文字表现尽可能多的内涵。这就是古人所说的“言简而意丰”和“言有尽而意无穷”。
(均根据相关材料改编)
19. 跨学科 数学 甲、乙两个小组汇报的观点之间是什么关系?下列图示中,最能体现这种关系的一项是
(
C
)(2分)
20. 甲组汇报中多处引用诗句作为材料证明观点。请选择我们学过的诗词,为汇报中的画线句子提供合适的论据,并加以简要分析,论证它的观点。(3分)
示例:“两个黄鹂鸣翠柳,一行白鹭上青天。”(杜甫《绝句》)这两句诗对仗工整,“两个”对“一行”,“黄鹂”对“白鹭”,“鸣翠柳”对“上青天”,通过简洁和谐的语言描绘出一幅富有生机的画面,体现了诗歌中“对仗”使意境优美、抒情感人的特点。
21. 从甲、乙两组中选择一组,结合“论证要合理”评价量表,任选两个角度,对该组所搜集的材料进行评价。(4分)

示例:甲组。
论证观点明确:围绕“数学与诗歌的共性”展开论述,观点清晰。
论证方法恰当:引用陆游、傅立叶等人的言论,运用举例论证(李白诗句)等,增强说服力。
22. 微写作 诗歌创作 请以“数学”为话题,参照下面的示例,参与文学社的诗歌创作征稿活动。要求:题目自拟,创作小诗,体现数学相关概念与生活的联系,不超过8行。(3分)

《平行线与生活》
生活如平行线
看似永不相交
却各自延伸
向着远方蔓延
虽无交集的点
却有相同的信念
在各自的轨迹
绽放独特的光焰
答案:
19. C
20. 示例:“两个黄鹂鸣翠柳,一行白鹭上青天。”(杜甫《绝句》)这两句诗对仗工整,“两个”对“一行”,“黄鹂”对“白鹭”,“鸣翠柳”对“上青天”,通过简洁和谐的语言描绘出一幅富有生机的画面,体现了诗歌中“对仗”使意境优美、抒情感人的特点。
21. 示例:甲组。
论证观点明确:围绕“数学与诗歌的共性”展开论述,观点清晰。
论证方法恰当:引用陆游、傅立叶等人的言论,运用举例论证(李白诗句)等,增强说服力。
论证思路清晰:先总述,再从四个方面分述,条理清楚。
22. 示例:
《平行线与生活》
生活如平行线
看似永不相交
却各自延伸
向着远方蔓延
虽无交集的点
却有相同的信念
在各自的轨迹
绽放独特的光焰
20. 示例:“两个黄鹂鸣翠柳,一行白鹭上青天。”(杜甫《绝句》)这两句诗对仗工整,“两个”对“一行”,“黄鹂”对“白鹭”,“鸣翠柳”对“上青天”,通过简洁和谐的语言描绘出一幅富有生机的画面,体现了诗歌中“对仗”使意境优美、抒情感人的特点。
21. 示例:甲组。
论证观点明确:围绕“数学与诗歌的共性”展开论述,观点清晰。
论证方法恰当:引用陆游、傅立叶等人的言论,运用举例论证(李白诗句)等,增强说服力。
论证思路清晰:先总述,再从四个方面分述,条理清楚。
22. 示例:
《平行线与生活》
生活如平行线
看似永不相交
却各自延伸
向着远方蔓延
虽无交集的点
却有相同的信念
在各自的轨迹
绽放独特的光焰
查看更多完整答案,请扫码查看


