第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2024广西南宁期中」如图,已知$AC⊥BC$于点C,$CD⊥AB$于点D,$∠A= 56^{\circ }$,则$∠DCB$的度数是(
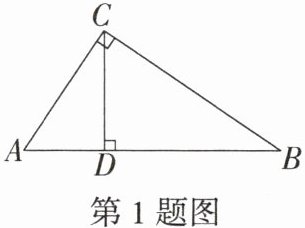
A.$30^{\circ }$
B.$45^{\circ }$
C.$56^{\circ }$
D.$60^{\circ }$
C
)
A.$30^{\circ }$
B.$45^{\circ }$
C.$56^{\circ }$
D.$60^{\circ }$
答案:
C
∵AC⊥BC,CD⊥AB,
∴∠ACB=∠ADC=90°.
∵∠A=56°,
∴∠ACD=90°−56°=34°,
∴∠DCB=90°−34°=56°. 故选C.
∵AC⊥BC,CD⊥AB,
∴∠ACB=∠ADC=90°.
∵∠A=56°,
∴∠ACD=90°−56°=34°,
∴∠DCB=90°−34°=56°. 故选C.
2.如图,直线$a// b$,将直角三角尺按如图所示的方式摆放,直角三角尺两个顶点分别在直线a,b上,则图中与$∠1$互余的角有( )

A.1个
B.2个
C.3个
D.4个

A.1个
B.2个
C.3个
D.4个
答案:
C 如图,
∵∠1+∠2=90°,
∴∠2与∠1互余,
∵∠2=∠3,
∴∠1+∠3=90°,即∠3与∠1互余,
∵a//b,
∴∠2=∠4,
∴∠1+∠4=90°,即∠4与∠1互余,
∴图中与∠1互余的角有3个,故选C.

C 如图,
∵∠1+∠2=90°,
∴∠2与∠1互余,
∵∠2=∠3,
∴∠1+∠3=90°,即∠3与∠1互余,
∵a//b,
∴∠2=∠4,
∴∠1+∠4=90°,即∠4与∠1互余,
∴图中与∠1互余的角有3个,故选C.

3.「2025河南郑州期中」如图,在$\triangle ABC$中,$∠C= 46^{\circ }$,$∠BAC= 80^{\circ }$,$\triangle ABC$的高AD和角平分线BE交于点F.求$∠AFE$的度数.
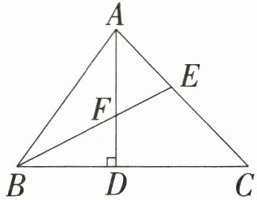
$∠AFE$的度数为

$∠AFE$的度数为
63°
.
答案:
解析
∵∠C=46°,∠BAC=80°,
∴∠ABC=180°−∠C−∠BAC=54°,
∵BE是∠ABC的平分线,
∴∠DBF=$\frac{1}{2}$∠ABC=27°,
∵AD是△ABC的高,
∴AD⊥BC,
∴∠BFD=90°−∠DBF=63°,由对顶角相等得∠AFE=∠BFD=63°.
∵∠C=46°,∠BAC=80°,
∴∠ABC=180°−∠C−∠BAC=54°,
∵BE是∠ABC的平分线,
∴∠DBF=$\frac{1}{2}$∠ABC=27°,
∵AD是△ABC的高,
∴AD⊥BC,
∴∠BFD=90°−∠DBF=63°,由对顶角相等得∠AFE=∠BFD=63°.
4.学科教材特色变式如图,点E是$\triangle ABC$中AC边上的一点,过E作$ED⊥AB$,垂足为D,若$∠1= ∠2$,则$\triangle ABC$是(
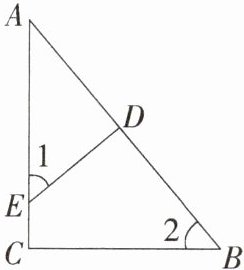
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法确定
A
)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.无法确定
答案:
A
∵ED⊥AB,
∴∠1+∠A=90°,
∵∠1=∠2,
∴∠2+∠A=90°,
∴∠ACB=90°,
∴△ABC是直角三角形. 故选A.
∵ED⊥AB,
∴∠1+∠A=90°,
∵∠1=∠2,
∴∠2+∠A=90°,
∴∠ACB=90°,
∴△ABC是直角三角形. 故选A.
5.如图,BD平分$∠ABC$,$∠ADB= 60^{\circ }$,$∠BDC= 80^{\circ }$,$∠C= 70^{\circ }$,则$\triangle ABD$是______三角形.
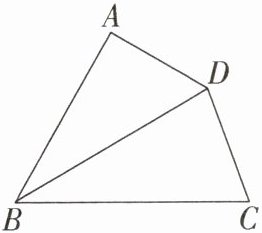

直角
答案:
答案 直角
解析 在△DBC中,∠BDC=80°,∠C=70°,
∴∠DBC=180°−80°−70°=30°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∵∠ADB=60°,
∴∠A=180°−30°−60°=90°,
∴△ABD是直角三角形.
解析 在△DBC中,∠BDC=80°,∠C=70°,
∴∠DBC=180°−80°−70°=30°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∵∠ADB=60°,
∴∠A=180°−30°−60°=90°,
∴△ABD是直角三角形.
6.「2024福建漳州一模,★☆」下列条件:①$∠A+∠B= ∠C$;②$∠A:∠B:∠C= 1:5:6$;③$∠A= 90^{\circ }-∠B$;④$∠A= ∠B= ∠C$.其中能确定$\triangle ABC$是直角三角形的条件有(
A.1个
B.2个
C.3个
D.4个
C
)A.1个
B.2个
C.3个
D.4个
答案:
C ①
∵∠A+∠B=∠C,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形;②
∵∠A:∠B:∠C=1:5:6,
∴设∠A=x,则∠B=5x,∠C=6x,
∴x+5x+6x=180°,
∴x=15°,
∴∠C=15°×6=90°,
∴△ABC是直角三角形;③
∵∠A=90°−∠B,
∴∠A+∠B=90°,
∴△ABC是直角三角形;④
∵∠A=∠B=∠C,
∴∠A=∠B=∠C=60°,
∴△ABC不是直角三角形. 综上所述,能确定△ABC是直角三角形的条件有①②③,共3个. 故选C.
∵∠A+∠B=∠C,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形;②
∵∠A:∠B:∠C=1:5:6,
∴设∠A=x,则∠B=5x,∠C=6x,
∴x+5x+6x=180°,
∴x=15°,
∴∠C=15°×6=90°,
∴△ABC是直角三角形;③
∵∠A=90°−∠B,
∴∠A+∠B=90°,
∴△ABC是直角三角形;④
∵∠A=∠B=∠C,
∴∠A=∠B=∠C=60°,
∴△ABC不是直角三角形. 综上所述,能确定△ABC是直角三角形的条件有①②③,共3个. 故选C.
7.「2025山西忻州期中,★☆」如图,小明在计算机上用“几何画板”画了一个$Rt\triangle ABC$,$∠C= 90^{\circ }$,并画出了两锐角的平分线AD,BE及其交点F.小明发现,无论怎样变动$Rt\triangle ABC$的形状和大小,$∠AFB$的度数是定值,则这个定值为(
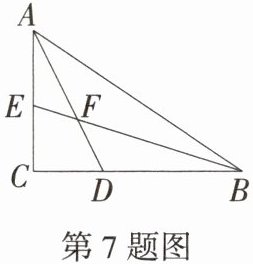
A.$135^{\circ }$
B.$150^{\circ }$
C.$120^{\circ }$
D.$110^{\circ }$
A
)
A.$135^{\circ }$
B.$150^{\circ }$
C.$120^{\circ }$
D.$110^{\circ }$
答案:
A
∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵AD平分∠CAB,BE平分∠ABC,
∴∠FAB=$\frac{1}{2}$∠CAB,∠FBA=$\frac{1}{2}$∠CBA,
∴∠FAB+∠FBA=$\frac{1}{2}$(∠CAB+∠CBA)=45°,
∴∠AFB=180°−45°=135°. 故选A.
∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵AD平分∠CAB,BE平分∠ABC,
∴∠FAB=$\frac{1}{2}$∠CAB,∠FBA=$\frac{1}{2}$∠CBA,
∴∠FAB+∠FBA=$\frac{1}{2}$(∠CAB+∠CBA)=45°,
∴∠AFB=180°−45°=135°. 故选A.
8.「2024四川凉山州中考,★☆」如图,$\triangle ABC$中,$∠BCD= 30^{\circ }$,$∠ACB= 80^{\circ }$,CD是边AB上的高,AE是$∠CAB$的平分线,则$∠AEB$的度数是______
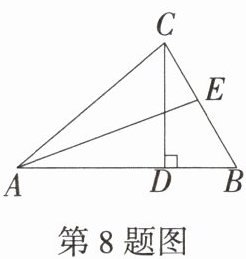
100°
.
答案:
答案 100°
解析
∵CD是边AB上的高,
∴∠CDB=∠CDA=90°,
∵∠BCD=30°,∠ACB=80°,
∴∠ACD=∠ACB−∠BCD=50°,∠CBD=90°−∠BCD=60°,
∴∠CAB=90°−∠ACD=40°,
∵AE是∠CAB的平分线,
∴∠EAB=$\frac{1}{2}$∠CAB=20°,
∴∠AEB=180°−∠EAB−∠EBA=100°.
解析
∵CD是边AB上的高,
∴∠CDB=∠CDA=90°,
∵∠BCD=30°,∠ACB=80°,
∴∠ACD=∠ACB−∠BCD=50°,∠CBD=90°−∠BCD=60°,
∴∠CAB=90°−∠ACD=40°,
∵AE是∠CAB的平分线,
∴∠EAB=$\frac{1}{2}$∠CAB=20°,
∴∠AEB=180°−∠EAB−∠EBA=100°.
9.如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ }$,点D在AB边上,将$\triangle CBD$沿CD折叠,使点B恰好落在AC边上的点E处.若$∠A= 25^{\circ }$,则$∠CDE= $______
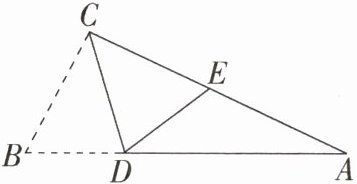
70°
.
答案:
答案 70°
解析
∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠B=∠CED,
∵∠A=25°,
∴∠B=90°−25°=65°,
∴∠CED=65°,
∴∠CDE=180°−45°−65°=70°.
解析
∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠B=∠CED,
∵∠A=25°,
∴∠B=90°−25°=65°,
∴∠CED=65°,
∴∠CDE=180°−45°−65°=70°.
查看更多完整答案,请扫码查看


