《2025年5年中考3年模拟八年级数学上册人教版》

1.「2025北京海淀质检」下列添括号错误的是(A)
A.$-x+5= -(x+5)$
B.$-7m-2n= -(7m+2n)$
C.$a^{2}-3= +(a^{2}-3)$
D.$2x-y= -(y-2x)$

答案： A $-x + 5 = -(x - 5)$，故A错误；B、C、D均符合添括号法则。故选A。

2.下列各式中,去括号或添括号正确的是(B)
A.$a^{2}-(b+c)= a^{2}-b+c$
B.$a-[1-(b+c)]= a+b+c-1$
C.$a-2x+y= a+(-2x-y)$
D.$x-a+y-b= (x+y)-(a-b)$

答案： B $a^{2} - (b + c) = a^{2} - b - c$，故A选项不符合题意。$a - [1 - (b + c)] = a + b + c - 1$，故B选项符合题意。$a - 2x + y = a + (-2x + y)$，故C选项不符合题意。$x - a + y - b = (x + y) - (a + b)$，故D选项不符合题意。故选B。

3.「2025广西南宁八中月考」下列添括号错误的是(D)
A.$3-4x= -(4x-3)$
B.$(a+b)-2a-b= (a+b)-(2a+b)$
C.$-x^{2}+5x-4= -(x^{2}-5x+4)$
D.$-a^{2}+4a+a^{3}-5= -(a^{2}-4a)-(a^{3}+5)$

答案： D $-a^{2} + 4a + a^{3} - 5 = -(a^{2} - 4a) - (-a^{3} + 5)$，D错误，符合题意。故选D。

4.在括号内填上适当的项.
(1)$a-2b+c+d= a-$(2b - c - d).
(2)$-a-3b+c= -$(a + 3b - c).
(3)$x^{2}-2y^{2}+2x-3y=$(x² - 2y²)$+2x-3y$.
(4)$x^{2}-y^{2}-x-y= x^{2}-x-$(y² + y).

答案： 答案
(1)$2b - c - d$
(2)$a + 3b - c$
(3)$x^{2} - 2y^{2}$
(4)$y^{2} + y$

5.学科教材 特色变式 计算:
(1)$(a+b-1)^{2}$.
(2)$(x-2y-1)^{2}$.
(3)$(a^{2}-a+1)(a^{2}+a+1)$.
(4)$(3m+2n-p)(3m-2n+p)$.

答案： 解析
(1)$(a + b - 1)^{2} = (a + b)^{2} - 2(a + b) + 1 = a^{2} + 2ab + b^{2} - 2a - 2b + 1$。
(2)$(x - 2y - 1)^{2} = (x - 2y)^{2} - 2(x - 2y) + 1 = x^{2} - 4xy + 4y^{2} - 2x + 4y + 1$。
(3)$(a^{2} - a + 1)(a^{2} + a + 1) = [(a^{2} + 1) - a][(a^{2} + 1) + a] = (a^{2} + 1)^{2} - a^{2} = a^{4} + 2a^{2} + 1 - a^{2} = a^{4} + a^{2} + 1$。
(4)$(3m + 2n - p)(3m - 2n + p) = [3m + (2n - p)][3m - (2n - p)] = (3m)^{2} - (2n - p)^{2} = 9m^{2} - 4n^{2} + 4np - p^{2}$。
#### 方法归纳
计算两个三项式相乘的方法
(1)有符号相同的，也有符号不同的两个三项式相乘，可通过变形用平方差公式计算。确定平方差公式中“$a$”“$b$”的方法：完全相同的项为“$a$”，绝对值相同且符号相反的项为“$b$”。
(2)两个因式中绝对值相同的各项，若符号全部相同或全部相反，可通过变形用完全平方公式计算。

6.学科易错题「2025河北廊坊月考,」若$(a^{2}+b^{2}+1)(a^{2}+b^{2}-1)= 35$,则$a^{2}+b^{2}=$(6)
A.3
B.6
C.±3
D.±6

答案： B $\because (a^{2} + b^{2} + 1)(a^{2} + b^{2} - 1) = 35$，$\therefore [(a^{2} + b^{2}) + 1] \cdot [(a^{2} + b^{2}) - 1] = (a^{2} + b^{2})^{2} - 1 = 35$，$\therefore (a^{2} + b^{2})^{2} = 36$，$\because a^{2} + b^{2} \geq 0$，$\therefore a^{2} + b^{2} = 6$。故选B。
#### 易错警示
本题易忽视$a^{2} + b^{2} \geq 0$而出错。

7.「2025河北廊坊月考,」当$x= -1$时,$ax+b+1$的值为-3,求$(a-b-1)(1-a+b)$的值.

答案： 解析 $\because$当$x = -1$时，$ax + b + 1$的值为$-3$，$\therefore -a + b + 1 = -3$，$\therefore -a + b = -4$，$\therefore a - b = 4$，$\therefore (a - b - 1)(1 - a + b) = [(a - b) - 1][1 - (a - b)] = (4 - 1) \times (1 - 4) = -9$。

8.新 代数推理「」若$m≠0,Q= (m^{2}-m+1)(m^{2}+m+1),P= (m+1)^{2}(m-1)^{2}$,猜想Q与P的大小关系,并证明你的猜想.
猜想Q与P的大小关系为Q＞P。证明如下：
$Q - P = (m^{2} - m + 1)(m^{2} + m + 1) - (m + 1)^{2}(m - 1)^{2} = (m^{2} + 1)^{2} - m^{2} - (m^{2} - 1)^{2} = (m^{2} + 1 + m^{2} - 1)(m^{2} + 1 - m^{2} + 1) - m^{2} = 4m^{2} - m^{2} = 3m^{2}$。
$\because m \neq 0$，$\therefore 3m^{2} ＞ 0$。$\therefore Q - P ＞ 0$。$\therefore Q ＞ P$。

答案： 解析 $Q ＞ P$。证明如下：
$Q - P = (m^{2} - m + 1)(m^{2} + m + 1) - (m + 1)^{2}(m - 1)^{2} = (m^{2} + 1)^{2} - m^{2} - (m^{2} - 1)^{2} = (m^{2} + 1 + m^{2} - 1)(m^{2} + 1 - m^{2} + 1) - m^{2} = 4m^{2} - m^{2} = 3m^{2}$。
$\because m \neq 0$，$\therefore 3m^{2} ＞ 0$。$\therefore Q - P ＞ 0$。$\therefore Q ＞ P$。

9.新课标 学科教材 抽象能力 特色变式 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了$(a+b)^{n}$(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应着$(a+b)^{2}= a^{2}+2ab+b^{2}$展开式中的系数;第四行的四个数1,3,3,1,恰好对应着$(a+b)^{3}= a^{3}+3a^{2}b+3ab^{2}+b^{3}$展开式中的系数等等.

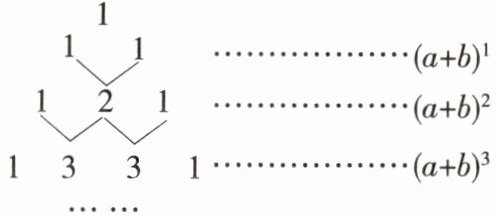
(1)根据上面的规律,写出$(a+b)^{6}$的展开式.
$(a+b)^{6}=$$a^{6} + 6a^{5}b + 15a^{4}b^{2} + 20a^{3}b^{3} + 15a^{2}b^{4} + 6ab^{5} + b^{6}$
(2)利用上面的规律计算:$2^{6}-6×2^{5}+15×2^{4}-20×2^{3}+15×2^{2}-6×2+1$.
1

答案： 解析
(1)$(a + b)^{6} = a^{6} + 6a^{5}b + 15a^{4}b^{2} + 20a^{3}b^{3} + 15a^{2}b^{4} + 6ab^{5} + b^{6}$。
(2)原式$=(2 - 1)^{6} = 1$。